Sustainable Value-based Management: Waardecreatie

Na het eerder gepubliceerde introductie artikel is dit het eerste in een reeks van vier inhoudelijke artikelen over Sustainable Value-based Management ofwel duurzame waarde-creatie. In dit artikel gaan we in op het concept van waardecreatie. Los van de vraag hoe we ‘waarde’ precies uitdrukken of meten, moet elke organisatie ten minste voor één iemand ‘nut’ hebben. Zonder enig zicht op ‘toegevoegde waarde’ – en dit geldt zowel voor de profit als de non-profit sector – is de moeite en energie die het kost om de organisatie zelf in stand te houden simpelweg een verspilling.

We lijken hierbij nog wel eens te vergeten dat ‘de waarde’ van een goed (of dienst) uiteindelijk samenhangt met mate waarin dat goed (of die dienst) in staat is om in de toekomst in menselijke behoeftes te voorzien. Je zou kunnen zeggen dat onze collectieve behoeftes (bijvoorbeeld gerangschikt volgens de piramide van Maslow) de intrinsieke waarde van producten en diensten drijft die organisaties voortbrengen. Eenvoudig gezegd, een organisatie heeft ‘nut’ wanneer er door toe doen van die organisatie in de toekomst meer menselijke behoeftes bevredigd kunnen worden dan zonder de aanwezigheid van die organisatie.

Bestaansrecht

Elke organisatie moet om haar bestaansrecht te behouden dus activiteiten blijven ondernemen welke – geconsolideerd gezien -naar verwachting ‘waarde’ genereren. De activiteiten moeten, bijvoorbeeld gemeten in tijd, energie, geld of plezier, naar verwachting méér opleveren in de toekomst dan we er vanaf nu nog in moeten stoppen. We moeten er dus nog bijvoorbeeld tijd, energie en geld instoppen, in de verwachting er later meer uit te kunnen halen. We geven dus enerzijds wat op, in de hoop er anderzijds later meer voor terug te krijgen. Er moet dus overall gezien sprake zijn van een toekomstig netto-rendement qua behoefte bevrediging. Alleen dan hebben de producten en diensten (en dus de organisatie zelf) inherent ‘nut’ ofwel rationeel gezien waarde.

Om ‘de waarde’ te kunnen bepalen is het dan wel cruciaal dat we niet alleen de mate van behoefte bevrediging aan de output kant meten, maar ook hetgeen we er aan de input kant in moeten stoppen. We komen er uitgebreid op terug in het eerstvolgende artikel als we ingaan op de verschillende waardeperspectieven, maar bij duurzame waardecreatie kijken we niet alleen naar het effect van de organisatie op de behoeften van haar klanten en eigenaren. Maar ook naar de waardecreatie (of het gebrek daaraan) voor medewerkers en de maatschappij als geheel.

Waarde toekomstgericht

Voor nu is het vooral belangrijk vast te houden dat ‘waarde’ per definitie toekomstgericht is. Het gaat bij ‘waarde’ om het verschil tussen wat we er vanaf nu nog in totaliteit in moeten stoppen en vanaf nu nog uit denken te kunnen halen. Waarde draait dus primair om verwachtingen omtrent de toekomst en niet om historisch behaalde resultaten!

We weten allemaal dat de toekomst onlosmakelijk met verandering verbonden is (“Panta Rhei”). En dat al onze huidige pogingen om waarde te creëren, dus plaatsvinden tegen de achtergrond van die continue veranderingen. Daarbij komt dat in de verandering onontkoombaar een bepaalde mate van natuurlijke willekeur inherent aanwezig is. Er bestaan in het hele universum voor zover we weten geen volledig deterministische processen, zo ook uiteraard niet binnen organisaties en economieën. Hoe goed we ons best ook doen, en welke preventieve of beheersmaatregelen we ook nemen, we zullen heel bescheiden moeten blijven en moeten leven met een bepaalde mate van onzekerheid in ieder proces en iedere activiteit die we ondernemen.

Uiteraard gaat die willekeur twee kanten op, het kan mee- of tegenzitten. En met elke activiteit die we ondernemen komt zo een kans op een positief, maar ook een risico op een negatief rendement.

De basisgedachte achter duurzame waardecreatie is dat een organisatie niet bestendig waarde kan realiseren voor één groep belanghebbenden, wanneer dat structureel ten koste gaat van een andere groep stakeholders. In het volgende artikel gaan we in op de verschillende perspectieven van waarde, op welke wijze deze uit te drukken en te meten. We laten zien hoe de perspectieven vaak samengaan, maar uiteraard soms ook conflicteren! Maar eerst gaan we in dit eerste artikel in op het creëren en realiseren van waarde, op de rol van verwachtingen en de onzekerheid die daar mee samenhangt, op kansen en risico’s en de samenhang tussen risico- en prestatiemanagement. We zullen nader ingaan op de begrippen risicocapaciteit en rendementseis en we zullen zien dat de relatie tussen risico’s, kansen en rendementen niet per definitie lineair verloopt. Deze basisuitgangspunten van waardemanagement zijn het beste uit te leggen aan de hand van een relatief eenvoudig voorbeeld.

Zeevissen?

Stel je bevindt je op een eiland ver weg, midden in de Grote Oceaan. Al zittend voor je zelfgebouwde boomhut en uitkijkend over de bruisende golven, overpeins je de twee opties die je op dit moment hebt. Veilig blijven zitten in de buurt van je boomhut of er met je houten bootje op uit trekken in een poging wat vis te vangen. Als je nu blijft zitten, zul je vanavond zeer waarschijnlijk wel nog leven, maar vrijwel zeker niets eten. Dat laatste is nog niet zo heel erg uiteraard, maar dat ga je ook geen dagen volhouden. Wanneer je er op uit trekt, loop je weliswaar gevaar, maar heb je ook een gerede kans wat voedzame vis te vangen. Met een stok teken je onderstaande figuur in het warme zand.

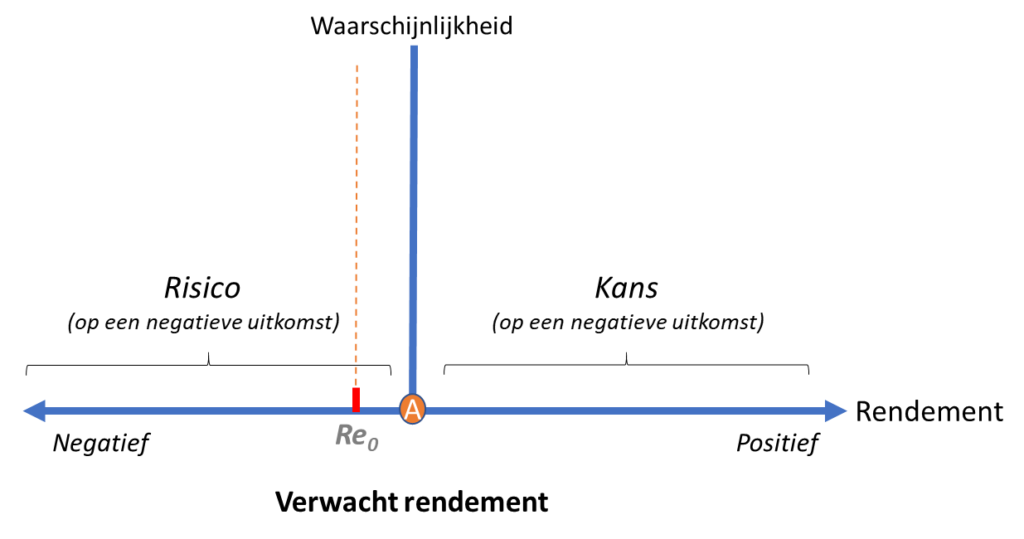
Op de X-as staat het verwacht rendement en op de Y-as de waarschijnlijkheid. Punt A vormt de oorsprong. Rechts van punt A op de X-as is het netto rendement positief en links ervan negatief. Je zou rechts net zo goed de kans-kant en links de risico-kant kunnen noemen. De activiteit waarbij je met je boot de zee op gaat in een poging vis te vangen, noem je alternatief A en het scenario waarbij je de rest van de dag relatief veilig voor je hutje blijft zitten, noem je alternatief 0. Je weet donders goed dat wanneer je niet gaat vissen, je niet zult eten, met als resultaat dat je met honger naar bed gaat. ‘Niets doen’ heeft dus wel degelijk consequenties!

Het netto rendement van ‘niets doen’ (Re₀) zal dus niet op de oorsprong (punt A), maar daar ergens links van liggen. In het 0-alternatief eet je die dag niet en lever je zogezegd eigenlijk in op je voedings- of energiebalans. Wanneer je inschat dat je minimaal 2 vissen per dag zult moeten eten om er qua voedingswaarde niet op achteruit te gaan, dan is het netto rendement van het 0-alternatief dus eigenlijk minus 2 vissen ofwel minus 2 voedingseenheden per dag.

Daarentegen biedt zeevissen (alternatief A) je de serieuze kans – maar uiteraard geen zekerheid – op het vangen van een paar voedzame vissen. Je denkt zelf per dag wel 5 vissen te kunnen vangen, maar weet ook dat het er op een goede dag 10, op een mindere dag 3 en op een slechte dag 0 zouden kunnen zijn. De vangst is per definitie onzeker. Met je houten bootje de zee op gaan, is bovendien niet zonder gevaar. Je kunt zomaar in een verraderlijke stroming terecht komen en wegdrijven van je eiland met z’n veilige boomhut. De boot kan lek slaan op de scherpe en ondiepe rotsen rondom. Er kunnen tijdens het vissen onverwacht haaien opduiken en in deze streek kan een flinke storm zo maar als uit het niets opsteken. Je kunt je zelf behoorlijk bezeren, gewond raken waardoor je een paar dagen niet kunt vissen of nog veel erger. En wanneer je een paar dagen niet zou kunnen vissen, verlies je uiteraard meer dan -2 voedingseenheden.

De uitkomst ofwel het rendement van de activiteit is onzeker en kan zowel links als rechts van de oorsprong liggen. Vandaar dat de X-as in het zandfiguur zowel aan de linker als rechterzijde onbegrensd is. Het verwacht rendement van alternatief A is dat je ’s avonds thuis komt met 5 heerlijke vissen. En ook al is het minder waarschijnlijk, de uitkomst kan ook 10, 20 of nog beter, dan wel 0 of nog veel slechter zijn. En zo teken je in het zand een waarschijnlijkheidscurve voor activiteit A. De waarschijnlijkheidscurve beschrijft per mogelijke uitkomst, dus per mogelijk punt op de X-as, de waarschijnlijkheid dat die uitkomst zich volgens jou zal voordoen.

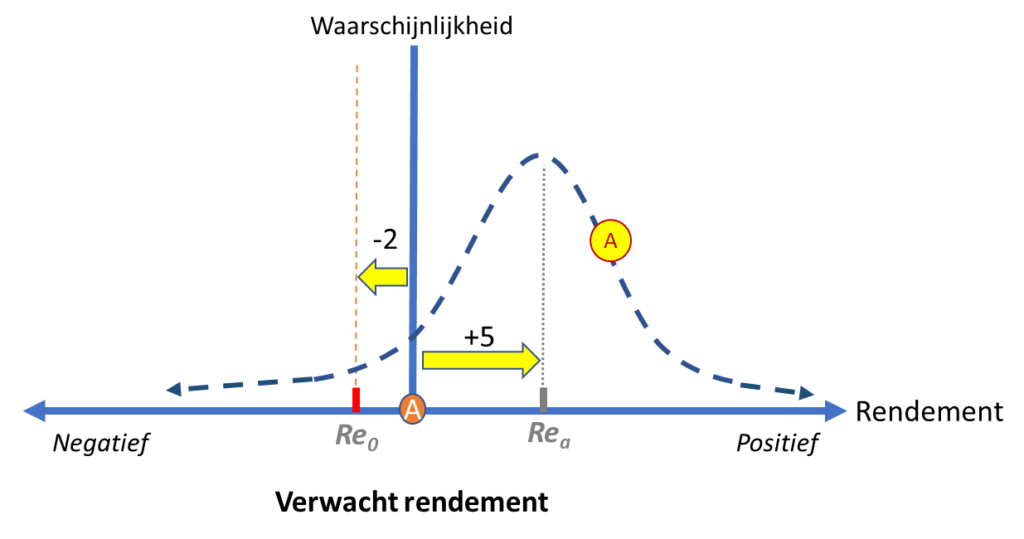
Wanneer je met de activiteit zeevissen naar verwachting 5 vissen, ofwel 5 voedingseenheden, denkt te gaan realiseren en met ‘niets doen’ (vrijwel) zeker 2 eenheden achteruit gaat, dan is je vergoeding voor het aangaan van de risico’s met zeevissen dus per saldo 7 eenheden. Uitgeschreven zou je kunnen zeggen:

Re_a = Re₀ + Specifieke risicovergoeding

Kijkend naar de figuur in het zand, merk je op dat de uitkomst van één dag vissen (alternatief A) slechter kan zijn dan de uitkomst van een dag niets doen (alternatief 0). Natuurlijk zul je voorzichtig zijn en bijvoorbeeld goed de getijde beweging en de wolkenlucht in de gaten houden, maar wanneer je kiest voor alternatief A moet je links- of rechtsom meer risico accepteren.

Kijkend naar je gammele houten bootje, vraag je jezelf af hoe ver je bereid bent hierin te gaan. Je allereerste gedachte is dat je op dit moment weinig trek hebt – en ook nog geen reden ziet – om een risico aan te gaan waarbij je zodanig ernstig gewond zou raken dat je een serieuze tijd niet kan vissen. Laten we dat operationaliseren en zeggen dat je vooralsnog geen risico wilt aangaan waardoor je 6 dagen of langer niet kunt gaan vissen. Je zou in die 6 dagen in totaal 12 voedingseenheden (2 per dag) achteruit gaan en dat beschouw jezelf wel zo’n beetje het maximaal draagbare verlies (alvorens je echt zou verzwakken en serieus gaat interen op je gezondheid).

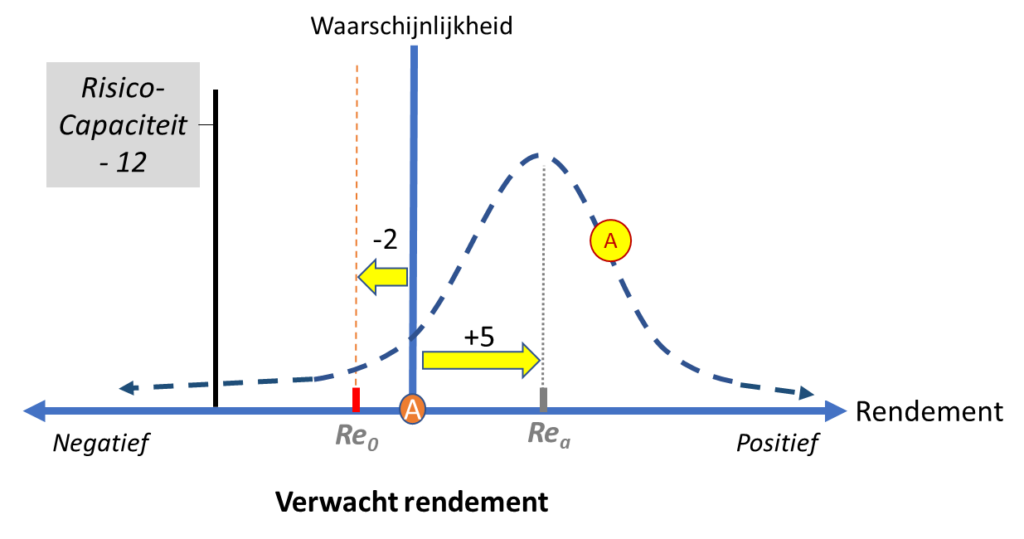
Kijkend naar het zandfiguur concludeer je dat activiteit A wel degelijk het risico bevat dat de uitkomst slechter dan -12 voedingseenheden zal zijn. Je acht het niet heel erg waarschijnlijk, maar ook niet onmogelijk.

Tegelijkertijd besef je dat je figuur een fout bevat. De uitkomst van alternatief 0 is weergegeven als een verticale lijn. Dat zou impliceren dat de uitkomst van ‘niets doen’ 100% zeker -2 voedingseenheden is, hetgeen haaks staat op de wetenschap (en levenservaring) dat niets ooit helemaal zeker is. Ook met alternatief 0 kun je door het toeval dom geluk of domme pech hebben. Een tornado kan plots opsteken en je boom met veilig geachte boomhut, omrukken en verwoesten. Een aardbeving kan een tsunami of landverschuiving veroorzaken. Je kunt ongetwijfeld zo nog een aantal scenario’s bedenken waarbij de uitkomst in positieve of negatieve zin zal afwijken van de verwachte -2. Het is niet waarschijnlijk, maar het ís mogelijk dat je aan het einde van een dag ‘niets doen’ moet concluderen dat je op die dag toch 12 of meer voedingseenheden hebt verloren….

De waarschijnlijkheidscurve van alternatief 0 is eigenlijk geen verticale lijn. Alle processen, hoe goed we ze ook denken te kunnen beheersen, kennen immers altijd een minimale mate van variantie. We kunnen het toeval nooit helemaal uitsluiten. Zeggen dat je géén risico groter dan -12 voedingseenheden wilt lopen, is feitelijk een onzinnige uitspraak! Je zult aan die grens ook een waarschijnlijkheid moeten koppelen. Je zou bijvoorbeeld kunnen zeggen dat je – uitgaande van de beperkt beschikbare informatie – niet meer dan 3% risico (=waarschijnlijkheid) wilt lopen op een verlies van 12 of meer voedingseenheden. Het gaat bij het evalueren van het risico (op een negatief rendement) of de kans (op een positief rendement) dus eigenlijk om het bepalen van de oppervlakte onder de waarschijnlijkheidscurve. Het voorbeeld gaat natuurlijk om het goede begrip van het concept, maar we moeten ons hierbij wel realiseren dat we in de praktijk de werkelijke vorm van de curve niet kennen!

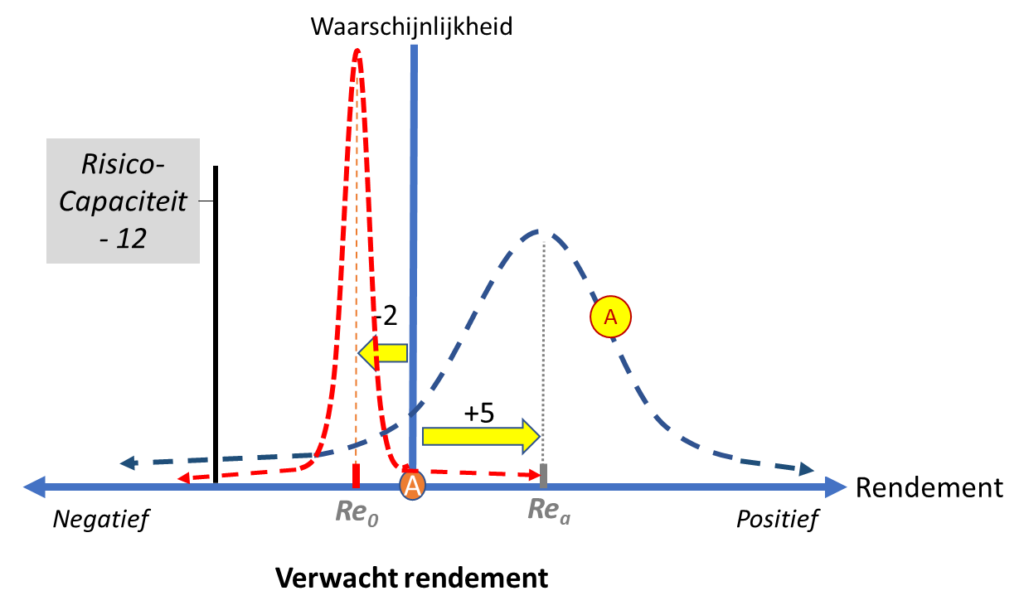
Wanneer je voor een een specifiek alternatief-scenario de waarschijnlijkheden van alle mogelijke uitkomsten op de X-as zou optellen, kom je tot 100% ofwel 1. Dit is gelijk aan het totale oppervlakte onder de curve. Stel dat we uit figuur 4 afleiden, dat ongeveer 5% van het oppervlakte onder de blauwe waarschijnlijkheidscurve van A links van de vastgestelde risico-capaciteit ligt. Je zou dan concluderen dat het risico van alternatief A te groot is (je had immers 3% als maximum gesteld). Je hebt dan iedere dag in de basis vier mogelijkheden:

• Je valt terug op alternatief 0 en doet die dag niks (wellicht in de hoop op een slimme ingeving of dat het toeval je later die dag geluk zal brengen);
• Je probeert iets te doen waarmee je de waarschijnlijkheidscurve van alternatief A spitser denkt te maken (bijvoorbeeld door je gammele boot met wat nieuwe planken en touw te verstevigen en voor jezelf een provisoir zwemvest te maken);
• Je probeert innovatief als je bent actief aan de slag te gaan met het bedenken van een derde alternatief; of
• Je past uiteindelijk toch maar je risico-tolerantie aan omdat je weet dat er geen enkel alternatief voorhanden is en alternatief 0 uiteindelijk tot een zekere dood zal leiden.

Een nieuw alternatief

Alhoewel we activiteiten moeten ontplooien om te overleven, kunnen we in het echte leven meestal niet alles (tegelijkertijd) ondernemen. Alleen al vanwege het simpele feit dat onze tijd op aarde beperkt en dus schaars is. We moeten meestal keuzes maken, dat merkt een ieder van ons dagelijks. Dat geldt ook voor organisaties. Aan de hoeveelheid beschikbaar geld, tijd, energie en andere productiefactoren zit altijd wel ergens een grens en deze zijn dus schaars. En wat geldt voor individuele consumenten, organisaties en overheden, geldt uiteindelijk ook voor economische systemen als geheel. En die collectieve schaarste nipt tot het maken van keuzes tussen alternatieve mogelijkheden binnen het systeem.

Terug naar ons simpele ‘gesloten’ economische systeem ergens op een eiland in de Grote Oceaan. Je hebt inmiddels de boot opgelapt en daarmee de waarschijnlijkheid op een negatieve uitkomst van 12 voedingseenheden of meer aanzienlijk beperkt. Alternatief A valt daarmee nu mooi binnen de vastgestelde risico-capaciteit. Maar tijdens het opknappen van je boot heb je nagedacht over een derde alternatief, namelijk ‘kokosnoten plukken’. Je weet dat je niet voor ‘zeevissen’ en ‘kokosplukken’ kunt kiezen vanwege bijvoorbeeld benodigde materialen, tijd, kennis en kunde. Stel je vindt ‘vis’ en ‘kokos’ even lekker, vissen even leuk als plukken en de benodigde investering in termen van tijd en energie is voor beide activiteiten even groot. Je weet dat blijvend ‘niets doen’ geen echte, bestendige optie is, op grond waarvan maak je dan een keuze tussen beide alternatieven?

Omdat we qua smaak geen voorkeur hebben voor zeevissen of kokos plukken, zal de keuze afhangen van de voedingswaarde die we denken met de beide activiteiten te kunnen behalen. Stel dat qua voedingswaarde 1 vis gelijk is aan 1 kokosnoot en dat we van beide onbeperkt kunnen blijven eten en genieten. In dat geval zullen we het verwacht rendement van beide activiteiten kunnen uitdrukken in equivalente aantallen. Het aantal vissen en het aantal kokosnoten dat we bijvoorbeeld met een dag werken verwachten te kunnen vangen dan wel plukken. We schatten in per dag 5 vissen of 8 kokosnoten te kunnen vangen dan wel plukken, dus Re_a = 5 en Re_b = 8 voedingseenheden. Zoals gezegd maakt het qua benodigde investering niet uit of we investeren in een boot met een visnet of in een ladder met enkele touwen. Welke activiteit heeft nu onze voorkeur? Om die vraag te kunnen beantwoorden moeten we een rendementseis (Re_eis) introduceren. Zou de rendementseis die we in dit voorbeeld stellen aan activiteit A gelijk zijn aan de rendementseis voor activiteit B? Of misschien beter gesteld, onder welke omstandigheid zou die rendementseis voor beide activiteiten gelijk zijn? Kijk eens naar figuur 5.

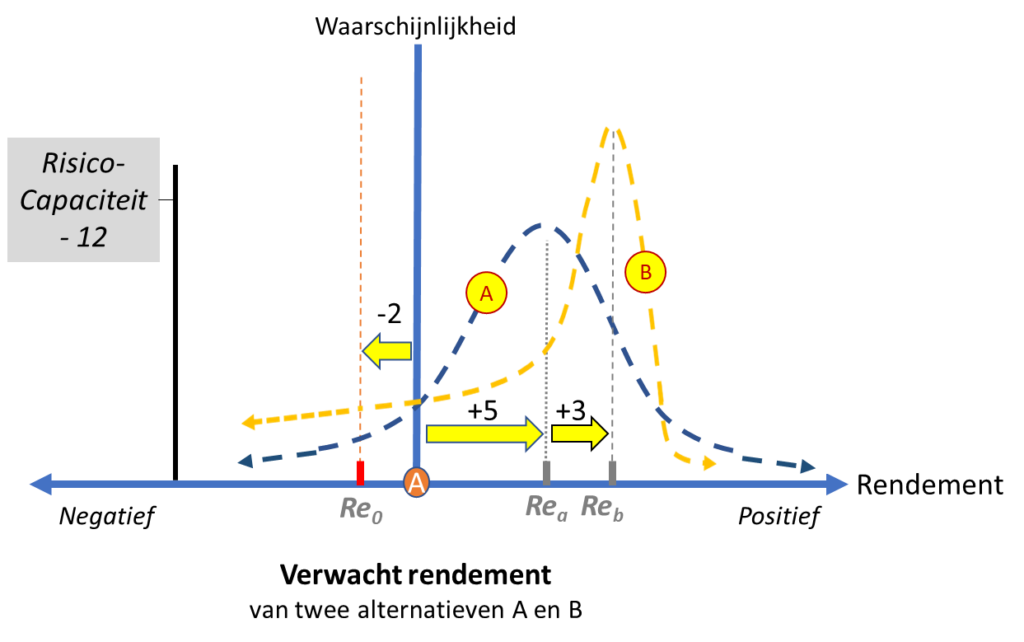
Activiteit A en B verschillen namelijk niet alleen qua verwacht rendement (Re_b > Re_a) maar ook qua spreiding van de mogelijke uitkomsten. De waarschijnlijkheidscurves van activiteit A en activiteit B zijn duidelijk verschillend. Uit figuur 5 kan afgeleid worden dat het risico op een negatieve uitkomst bij activiteit B (kokos plukken) groter is dan voor activiteit A (zeevissen). De oppervlakte onder de curve B aan de linkerzijde van de oorsprong is namelijk duidelijk groter dan de oppervlakte onder curve A. Zou je dan aan beide activiteiten dezelfde rendementseis moeten stellen? Omdat het risico voor beide activiteiten verschilt, zou een rationele benadering zijn om voor elk van de twee activiteiten een eigen rendementseis (Re_{eis A} en Re_{eis B}) te hanteren waarin het activiteit-specifieke risico is meegewogen.

Stel dat we uit figuur 5 concluderen dat het risico (op een negatief rendement) van activiteit B ongeveer 2 keer zo hoog is als voor activiteit A. Dan zullen we voor dat ‘extra risico’ van B eigenlijk ook een ‘extra rendement’ willen zien ten opzichte van activiteit A. Re_{eis B} zal afhangen van het relatieve risico van B ten opzichte van A alsmede van het verwachte rendement van A. De 5 voedingseenheden die activiteit A naar verwachting zal opleveren vormt als het ware het vertrekpunt voor de eis die we aan B zullen stellen. In elk geval zal, rationeel gezien, daarbij gelden dat Re_{eis B} > Re_A. De toeslag die we eisen voor het extra risico dat we lopen met activiteit B ten opzicht van het alternatief A, zal gebaseerd zijn op de risicovergoeding van activiteit A. De risicovergoeding voor alternatief A ten opzichte van het vrijwel risicoloze alternatief 0 (‘niets doen’) bedroeg 7 voedseleenheden. Het risico van B is ongeveer 2 keer het risico van A, we mogen dus verwachten dat de vereiste risicovergoeding voor B twee keer de risicovergoeding van A bedraagt.

Re_B =    Re₀ + Specifieke risicovergoeding voor B

       =    Re₀ + 2 x Specifieke risicovergoeding voor A

Het is eenvoudig te herleiden dat de rendementseis voor alternatief B dan 12 voedingseenheden zal zijn (immers: -2 + 2*7). De op het risico gebaseerde rendementseis is duidelijk hoger dan de verwachte vergoeding voor alternatief B. Mits beide alternatieven vallen binnen de gestelde risico-capaciteit, verdient Alternatief A dus de voorkeur boven alternatief B. Het hogere rendement van B weegt vooralsnog niet op tegen het hogere risico dat we lopen.

Natuurlijk drukken we het rendement normaal gesproken niet uit in kokosnoten of vis, maar in een percentage dat de verhouding tussen de in- en output weergeeft. Als we ergens bijvoorbeeld in totaal 100 euro in zouden kunnen investeren wat per jaar naar verwachting 5 euro oplevert, is het verwacht rendement 5%. Zou, gegeven het risico, de rendementseis bijvoorbeeld 7% bedragen, dan zouden we met deze investering waarde vernietigen. Niet doen dus. Bedraagt de risicoafhankelijke rendementseis voor deze investering bijvoorbeeld 3% dan zou de investering waarde realiseren. Deze investering is dan, gegeven het gepercipieerde risico, relatief aantrekkelijk ten opzichte van alternatieve investeringen. Feitelijk net zo als in ons voorbeeld bij zeevissen versus kokosnoten plukken. En ook in de werkelijke wereld zoeken we naar een ‘veilig alternatief’ om de risicovrije vergoeding te bepalen (in het Engels de risk-free rate genoemd) en kalibreren we vervolgens het te eisen rendement op een voorgenomen investering met de risico’s en rendementen van andere investeringsmogelijkheden die beschikbaar zijn in de markt.

Kans en risicomanagement

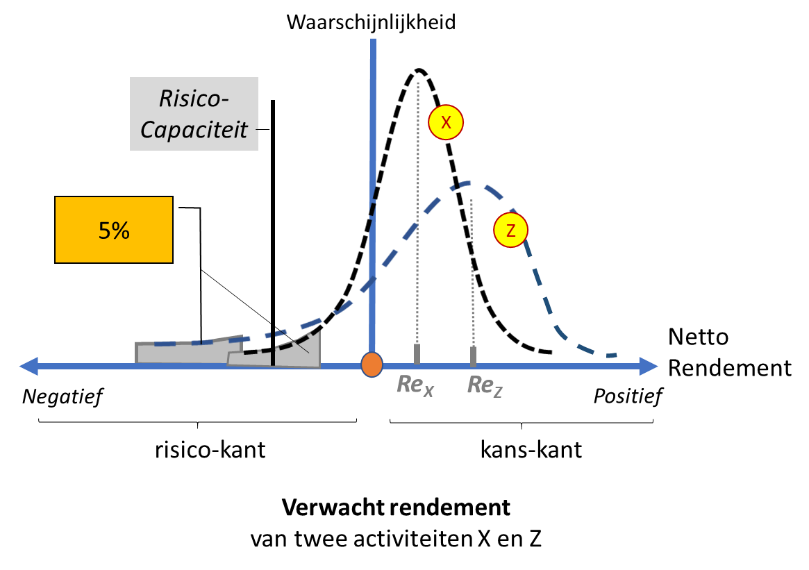
In figuur 6 hieronder zien we de verwachte rendementen (Re_X en Re_Z) voor twee mogelijke projecten X en Z alsmede de twee bijbehorende waarschijnlijkheidscurves. Voor project Z geldt zoals in de figuur te zien is dat meer dan 5% risico bestaat dat de uitkomst slechter is dan de vastgestelde risicocapaciteit. Voor project X geldt dat minder dan 5% van het oppervlakte van de curve links van de risicocapaciteit ligt. Het risico dat de uitkomst van project X negatiever wordt dan de risicocapaciteit wordt dus minder dan 5% geacht.

Vaak is het overzichtelijker om bovenstaande figuur net wat anders te presenteren door de linkerzijde van de X-as ‘omhoog’ te klappen.

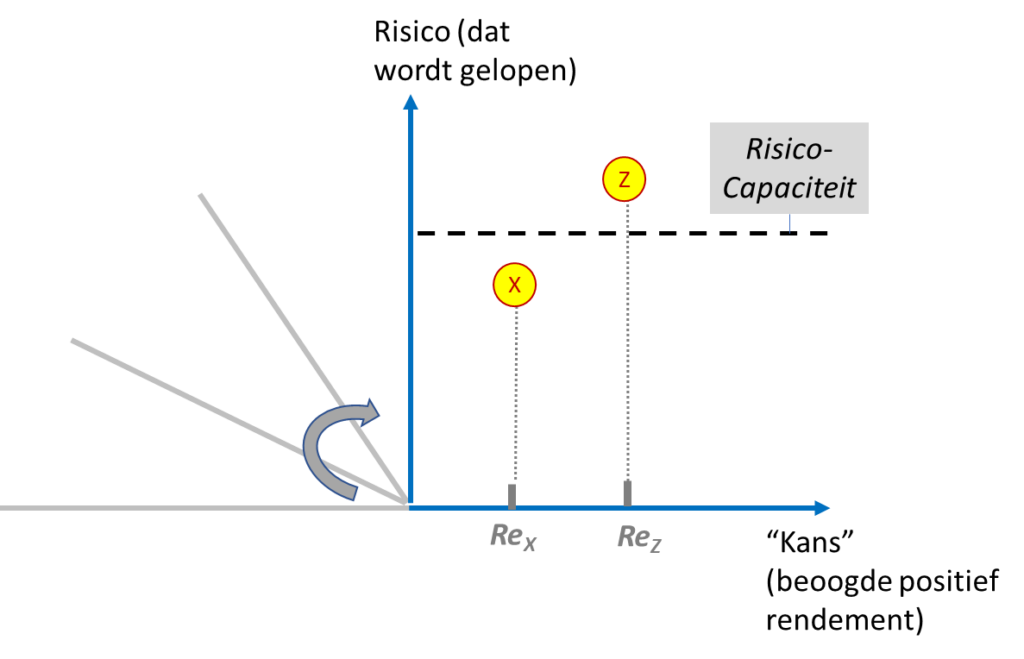
De X-as representeert de ‘kans’ die de activiteit of investering ons biedt, nog steeds uitgedrukt in het verwachte of beoogde positieve rendement. De Y-as drukt echter niet langer de waarschijnlijkheidsverdeling uit, maar het risico op een negatieve uitkomst. We markeren op de Y-as alleen het (in dit geval) 5%-risicopunt. Gegeven de waarschijnlijkheidsverdeling bestaat er dus een risico van 5% dat de uitkomst slechter zal zijn dan dat verlies. Hoe hoger dat punt op de Y-as ligt, des te risicovoller een project of alternatief dus is. Je zou dat punt ook kunnen zien als de uitkomst van het meest ongunstige scenario dat we nog realistisch achten, in de investeringsanalyse vaak het ‘worse-case’ scenario genoemd. Voor het goede begrip, wat zou er gebeuren als we niet het 5% maar het 1% punt zouden nemen? Zou dat punt dan omhoog of omlaag langs de Y-as bewegen?

Over het 5% risicopunt zou je ook kunnen zeggen dat er, wederom gegeven de waarschijnlijkheidscurve, 95% kans bestaat dat de uitkomst beter zal zijn dan die negatieve uitkomst. Vaak noemen we het risicopunt ook wel kortweg “het risico”. Je spreekt dan over “het risico” (aangegeven op de Y-as) van en “het verwacht rendement” (aangegeven op de X-as) van project X en Z. Wij weten nu dat achter die uitspraak een waarschijnlijkheids-verdeling schuilgaat, welke zowel qua kans op een positief rendement als risico op een negatief rendement niet begrenst is. Wanneer we nu naast de risico-capaciteit op de Y-as ook nog de rendementseis op de X-as zouden weergeven, dan krijgen we figuur 8 hieronder.

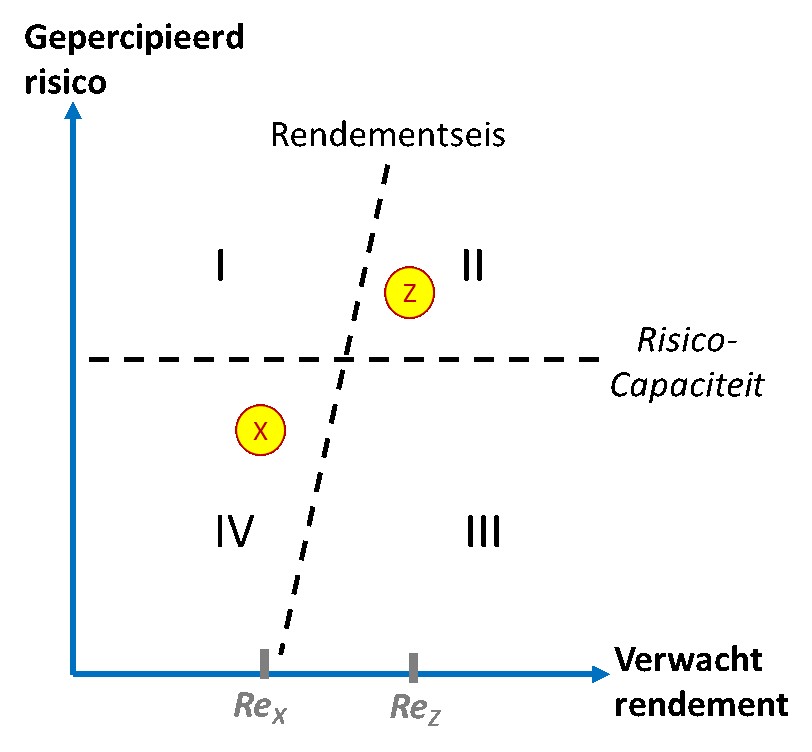
In figuur 8 zijn vier kwadranten te onderkennen. In kwadrant I is het netto rendement negatief en is het risico groter dan het maximaal te accepteren risico. Wanneer een voorgenomen activiteit zich inderdaad in dit kwadrant zou bevinden, zou het beter zijn om er van af te zien Met andere woorden, de activiteit voegt geen waarde toe aan de organisatie die deze ontplooit. In kwadrant II, waar project Z zich bevindt, is het risico weliswaar te hoog, maar wordt wel een positief netto rendement verwacht. In dit geval zou men op zoek kunnen gaan naar een manier om het risico te verlagen c.q. onder de maximale grens te brengen. Normaliter zal zo’n strategie wel extra tijd, energie of geld kosten en dus ten laste van het rendement gaan, maar die ‘ruimte’ is er ook gezien het thans positieve verwachte rendement. In kwadrant III is het verwacht netto rendement voldoende positief en ligt het gepercipieerde risico lager dan het maximaal te accepteren risico. Een voorgenomen activiteit of investering die in dit kwadrant zit, is dus de moeite waard. Een activiteit of investering in kwadrant IV, zoals project X, heeft weliswaar een negatief netto-rendement, maar het risico is lager dan het maximaal te accepteren risico. Wellicht kunnen we daar dus wat scherper aan de wind gaan zeilen, iets minder voorzichtigheid inbouwen om zo de rendementseis te halen.

Waarderealisatie en waardecreatie?

Tot nu toe spraken we steeds over voorgenomen activiteiten, voorgenomen projecten of investeringen en over het verwacht rendement. We kunnen natuurlijk ook achteraf kijken naar het daadwerkelijk rendement dat met een activiteit of project is gerealiseerd. Wanneer het rendement van een activiteit of project achteraf beter blijkt te zijn dan de vooraf gestelde risicoafhankelijke rendementseis, dan zeggen we dat die activiteit of dat project waarde heeft gerealiseerd. Waarderealisatie hangt dus samen met het achteraf (=ex post) wel of niet behalen van de vooraf (=ex ante) gestelde rendementseis. Waar we tot nu toe spraken over één activiteit kunnen we binnen een organisatie natuurlijk ook spreken over een cluster van activiteiten georganiseerd of samengebracht in bijvoorbeeld een vennootschap, Business Unit of product-markt combinatie (PMC’s).

Stel dat we de economische waarde van bijvoorbeeld verschillende Business Units willen plotten in de grafiek hieronder. We gaan in het volgende artikel in op de verschillende perspectieven van waarde en hoe deze uit te drukken en te meten. Een van de vier perspectieven die we zullen behandelen zal de economische waarde zijn. Die we “Value to the Firm” (VtF) zullen noemen. We bekommeren ons nu echter nog even niet hoe de economische waarde (VtF) en het economisch rendement van de BU’s te bepalen, dat volgt volgende keer, maar veronderstellen het rendement nu gewoon bekend. Het gerealiseerde economisch rendement wordt bijvoorbeeld per BU uitgezet op de X-as tegen het daarbij gelopen risico op de Y-as. Veel ondernemingen hanteren – voor het gemak – slechts een uniforme rendementseis voor al hun investeringen en kalibreren deze niet voor het specifieke risico. In dat geval loopt de rendementseis zoals in onderstaande figuur uiteraard verticaal parallel aan de Y-as.

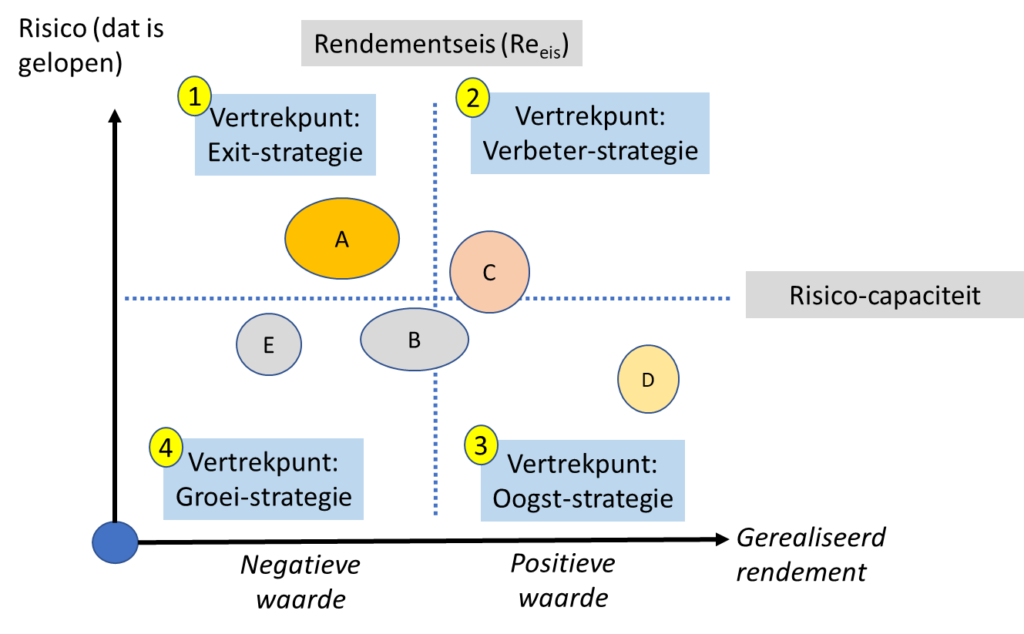
Elke BU valt dan in een van de vier kwadranten. Valt de BU in kwadrant I of IV dan is er sprake van een negatieve waarde en dus waarde-vernietiging (de rendementseis wordt immers niet behaald). Wordt de BU in kwadrant II of III geplaatst dan wordt waarde gerealiseerd, want de werkelijke prestaties overstijgen de vooraf vastgestelde rendementseis. Door de BU’s in de kwadranten te plotten ontstaat een plaat die prima aangewend kan worden om een strategische discussie te initiëren. Zeker als de rendementen over meerdere jaren in ogenschouw worden genomen.

Als aftrap voor een strategische discussie zou op hoofdlijnen voor elk van de vier kwadranten eigenlijk een verschillend vertrekpunt ingenomen kunnen worden: een “Exit-strategie” voor kwadrant I, een “Verbeter-strategie” voor kwadrant II, een “Oogst-strategie” voor kwadrant III en een “Groei-strategie” voor kwadrant IV. Maar eerst even een ‘reality check’. In bovenstaande figuur zijn vijf BU’s geplot (A tot en met E). De omvang van de bol zegt iets over de grootte van de desbetreffende BU. Stel u zit in de directie, op welke BU zou u als eerste de focus leggen?

Als u het betoog over de samenhang tussen risico en rendement – en tussen risico- en prestatiemanagement – echt heeft begrepen, zult u op het eerste oog concluderen dat met name BU D uit de toon valt. Een buitengewoon goed rendement tegen een zéér laag risico. Op het moment dat we zeggen dat risico en rendement samengaan, is dat opvallend en het nader onderzoeken meer dan waard.

Tot slot: Waardecreatie

Tot slot van dit artikel komen we dan eindelijk bij waardecreatie. Waar waarderealisatie iets zegt over de prestaties over de afgelopen periode, zegt waardecreatie iets over de verbetering of verslechtering. Onthoud dat waardecreatie altijd gaat over de stap ofwel de delta. Wanneer de gerealiseerde economische rendementen over twee opeenvolgende jaren 5% (Re_t=0) en 7% (Re_t=1) zouden zijn dan is er dus sprake van een positieve stap en dus sprake van waardecreatie. Waardecreatie zegt dus niets over het feit of de BU waarde heeft gerealiseerd. In het voorbeeld zou de rendementseis (Re_eis) bijvoorbeeld voor beide jaren 8% kunnen zijn geweest. De BU vernietigt dan in beide jaren waarde (= negatieve gerealiseerde waarde). Maar omdat jaar 1 beter is dan jaar 0 is er sprake van een verbetering en dus is sprake van waardecreatie.

De focus bij waardecreatie (value creation) ligt primair op het realiseren van die positieve stap, dus bij de verbetering! Let wel, omdat rendement een verhoudingsgetal is (tussen de totale investering en wat die investering over een bepaalde periode gezien oplevert), kun je het rendement verbeteren door ofwel de opbrengst te verbeteren dan wel door de totale investering te verlagen!

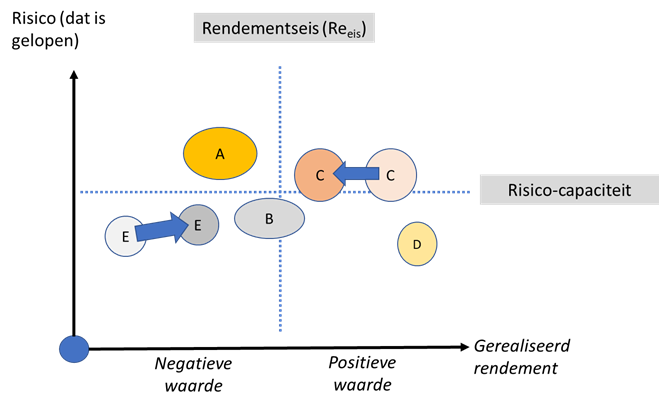
In figuur 10 hieronder zijn de rendementen voor BU C en BU E van dit jaar en vorig jaar aangegeven. Bij BU C moeten ondanks de positieve waarderealisatie toch flink de alarmbellen afgaan. Er is namelijk sprake van een serieuze verslechtering. Bij BU E zien we daarentegen juist een verbetering ondanks het feit dat er nog steeds geen sprake is van waarderealisatie. BU E moet vooral op de ingeslagen weg verder gaan. Het management van BU E verdient zo te zeggen een schouderklopje en verdere ondersteuning. Samen met het management van BU C moet serieus nagegaan worden hoe het tij te keren. Bij BU E is in tegenstelling tot BU C sprake van waardecreatie.

Binnen Sustainable Value-based Management erkennen we dat waarde vanuit meerdere perspectieven benaderd kan en moet worden. Economische waarde (Value to the Firm) is daar een van. Klanten, medewerkers en de maatschappij als geheel hanteren uiteraard andere ‘maatstaven’, maar feitelijk kunnen we ook voor deze ‘stakeholders’ het rendement en risico op vergelijkbare wijze uitdrukken en inzichtelijk maken. Hier komen we in het vervolgartikel uitgebreid op terug.

Samenvatting

Laten we tot slot de belangrijkste punten uit dit artikel samenvatten:

1. Iedere voorgenomen activiteit (of cluster van activiteiten) kent een kans op een positief rendement en een risico op een negatief rendement. Dus kansen en risico’s zijn inherent met elkaar verbonden (vanwege de activiteit waar aan ze ontspruiten) en vormen twee zijden van één en hetzelfde muntje;
2. Er bestaat altijd de mogelijkheid tot ‘niets doen’ (ofwel door te gaan op huidige voet), maar dit zogenaamde 0-alternatief heeft ook consequenties en dus een positief dan wel negatief verwacht rendement.
3. ‘Niets is zeker’, voor elk beschikbaar alternatief (ook het 0-alternatief!) geldt dat de inherente onzekerheid omtrent het ‘verwacht rendement’ beschreven kan worden door een waarschijnlijkheidsverdeling (de uitkomst is vooraf nooit 100% te garanderen);
4. ‘Alles is mogelijk’ en als je tijdshorizon maar lang genoeg is, zal iedere mogelijke uitkomst zich op enig moment ook daadwerkelijk voordoen. Met andere woorden, het zijn eigenlijk onze eigen verwachtingen die ons verrast doen staan;
5. De te stellen rendementseis aan een specifiek alternatief zou moeten samenhangen met het specifieke risico van de desbetreffende voorgenomen activiteit of investering (en dus niet met de generieke rendementseis van de investeerder zoals we wel vaak zien in de praktijk);
6. Er is geen absolute maatstaf, maar omdat alternatieven met elkaar concurreren (bijvoorbeeld om schaars beschikbare tijd, geld of energie) kunnen we de rendementseis voor een specifiek alternatief bepalen door een vergelijking met de verwachte rendementen en gepercipieerde risico’s van alternatieven;
7. Risico en rendement, en dus waarde, zijn relatieve begrippen. Het beoordelen van het verwacht rendement en het daaraan gerelateerde risico van een activiteit, project of investering vergt dus een vergelijking met het rendement en risico van minimaal een ander beschikbaar alternatief (ook al is dat het 0-alternatief);
8. De waarde van iets ligt opgesloten in de toekomst en kan gedefinieerd worden als het verschil tussen wat we er aan investering in totaal in moeten stoppen en wat we denken er straks uit te kunnen halen. Omdat waarde in de toekomst ligt, speelt onzekerheid een cruciale rol;
9. Gerealiseerde waarde kijkt terug en volgt uit het verschil tussen het gerealiseerde rendement en de rendementseis te vermenigvuldigen met de totale gedane investering. Waardecreatie draait om de verbeterstap in de gerealiseerde waarde. Een unit die waarde vernietigt in enig jaar kan toch verbeterd zijn en dus waarde hebben gecreëerd;
10. Waarde kan vanuit verschillende perspectieven bekeken worden. Sustainable Value-based Management gaat er vanuit dat een organisatie waarde moet creëren voor alle stakeholders om haar bestaansrecht op de lange termijn veilig te stellen. Een organisatie kan niet bestendig op de pof leven.

Lees ook de inleiding op dit artikel:

• Sustainable Value-based Management: Never Waste A Good Crisis! (longread)

Door: Stephan van den Broek, augustus 2020.

Met bijzondere dank aan Cor Rosbeek en Ramond Leenders voor hun waardevolle commentaar, vragen en adviezen.

---