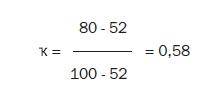‘Meten is weten’, zo luidt het adagium, maar is dat wel zo? Wel als je weet wát je meet. Dan is de vraag of de uitkomst van die meting herhaalbaar of reproduceerbaar is. Om die vraag te beantwoorden zijn diverse methoden ontwikkeld om daar een statistisch antwoord op te geven. Dus geen ja of nee, maar bijvoorbeeld ‘in hoge mate’.
Die herhaalbaarheid of reproduceerbaarheid heeft vooral te maken met de variatie die in het meetproces aanwezig is. Bij herhaalbaarheid wordt hetzelfde ding gemeten met hetzelfde meetinstrument en door dezelfde persoon. Bij reproduceerbaarheid gaat het juist om de vraag of je dezelfde resultaten zou krijgen als je iemand anders dezelfde meting zou laten uitvoeren.
Bij herhaalbaarheid wordt hetzelfde gemeten, met hetzelfde meetinstrument, door dezelfde persoon. Bij reproduceerbaarheid gaat het om de vraag of je dezelfde resultaten zou krijgen als iemand anders dezelfde meting zou uitvoeren.
Meetsysteemanalyse
Voor metingen met een meetapparaat, zoals een schuifmaat of een weegapparaat, waarbij je continu grootheden meet als lengte, gewicht, droge-stofgehalte, eiwitgehalte en dergelijke, bestaan gestandaardiseerde methoden, de zogenoemde meetsysteemanalyse. Door optredende variatie zouden de oordelen weliswaar iets van elkaar kunnen verschillen, maar er wordt niet naar de persoonlijke mening gevraagd.
Dat is wel het geval als de meting bestaat uit het persoonlijke oordeel van degene die de beoordeling uitvoert. Denk hierbij aan visuele controles en beoordelingen van dossiers. De centrale vraag is of de beoordelaars in zekere mate overeenstemmen in hun oordeel. De methode die we hier bespreken gaat uit van een dichotoom antwoord: goed of fout, ja of nee.
Bij een meting waar een persoonlijk oordeel aan gegeven wordt, is de vraag of de beoordelaars in zekere mate overeenstemmen in hun oordeel.
Veronderstel dat je een product hebt waar visueel merkbare beschadigingen op kunnen komen. Of een schoonmaakdienst wiens werk je moet controleren. Je laat het werk (product, schoongemaakte ruimte) door een beoordelaar visueel inspecteren. Hopelijk zijn er voor deze beoordelingen standaarden vastgelegd. Als dat niet zo is, wordt de variabiliteit alleen maar groter – en het gesprek over de resultaten van de meetmethodebeoordeling ook lastiger.
Voorbeeld: schoonmaakdienst
We nemen de schoonmaakdienst als voorbeeld. Een kantoor wordt schoongemaakt en op steekproefbasis worden de schoongemaakte kantoorkamers beoordeeld door een inspecteur. Deze geeft in eerste instantie aan of de kamer goed schoon is of niet. (Daarna wordt ook aangegeven wat er eventueel niet goed is, maar dat is voor de verklaring van de beoordeling.)
Er zijn meerdere inspecteurs en we nodigen er twee uit om te kijken in welke mate zij overeenstemmen in hun oordeel. Daarvoor selecteren we 40 kamers en sturen we de inspecteurs (in willekeurige volgorde, zonder dat ze het van elkaar weten en zonder dat ze de toestand van de schoongemaakte kamers beïnvloeden) op pad. Per kamer vragen we aan de beide inspecteurs wat hun oordeel is. De combinatie van deze oordelen turven we in een 2×2-matrix.
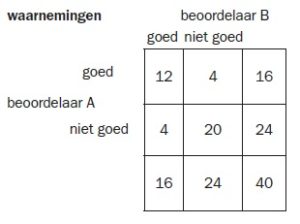
Stel dat we 40 kamers laten onderzoeken en dat we de volgende resultaten hebben in de 2×2-matrix.
Met deze 2×2-matrix moeten we drie dingen berekenen:
- Wat is de mate van overeenstemming? In de tabel wordt duidelijk dat er 32 keer overeenstemming is (goed-goed en niet goed-niet goed). Dat is 32 / 40 = 80%.
- In het geval van perfecte overeenstemming treedt alleen maar goed-goed en niet goed-niet goed op. Het percentage is dan 100%.
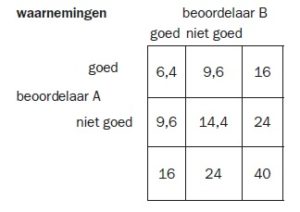
- In het geval dat de beoordelaars geen gelijkgestemd referentiekader hebben en dus geheel onafhankelijk van elkaar beoordelen, moeten we de mate van overeenstemming uitrekenen. Dat gaat via de volgende redenering, uitgaande van de randtotalen: stel dat beoordelaar A op een geheel andere wijze beoordeelt dan beoordelaar B, dan zou hij de kamers die door beoordelaar B als goed zijn beoordeeld, volgens de verhouding van de randtotalen beoordelen.
Beoordelaar A keurt er 16 van de 40 goed en 24 van de 40 niet goed. Dus bijvoorbeeld van de 16 kamers die door B als goed zijn beoordeeld, zou A er 16 / 40 * 16 = 6,4 goedkeuren en 24 / 40 * 16 als niet goed beoordelen. (Dit zijn natuurlijk rekenkundige resultaten, je kunt geen 0,2 kamer goedkeuren). Datzelfde geldt voor de kamers die door beoordelaar B als niet goed zijn beoordeeld. Dan ziet de 2×2-matrix er als volgt uit en volgt een overeenstemmingspercentage van (6,4 + 14,4) / 40 = 52%:
Cohen’s kappa
Een zekere heer Cohen heeft op basis van deze overweging een overeenstemmingsmaat gemaakt, de Cohen’s Kappa. Deze maat kijkt naar het verschil tussen waargenomen overeenstemming en willekeur en vergelijkt dat met het verschil tussen perfecte overeenstemming en willekeur.
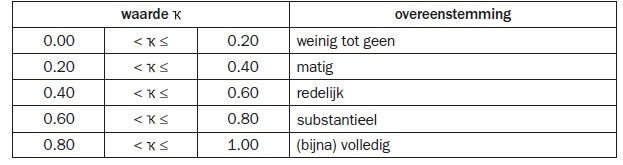
Deze waarde moet worden vergeleken met een tabelwaarde, die eruitziet zoals in de tabel hieronder.
Het is een eenvoudige procedure. Zie de uitkomst als indicatief, het is geen resultaat dat op 0,1 nauwkeurig is te interpreteren. Het is meer een redelijk onderbouwd beoordelingsresultaat dat aanleiding kan zijn tot een interessant gesprek.
Overeenstemming bereiken
Als er meerdere beoordelaars zijn, kun je hen paarsgewijs vergelijken om zo tot een aardige indicatie van overeenstemming te komen. Het zou ook mogelijk zijn om een standaard te creëren. Daarvan weet je dan of het goed of niet goed is en kun je de beoordelaars vergelijken met een standaard. Dat geeft ook een indicatie of een waarnemingsstandaard wel goed hanteerbaar is. Als er dan nog veel verschil zit in de mate van overeenstemming, geeft die standaard daarvoor nog te veel ruimte. Ook kun je op deze wijze de consistentie van beoordelaars onderzoeken, door ze (zonder dat ze het weten) twee keer hetzelfde object te laten beoordelen.
door Arend Oosterhoorn, zelfstandig kwaliteitsadviseur.