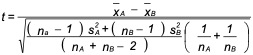
Stel je wil nagaan of een verbetering die je hebt doorgevoerd het verwachte resultaat oplevert. Of je moet beslissen of je overstapt naar een alternatieve leverancier. Dit soort vragen wordt veelal in algemene termen geformuleerd en de beslissing moet genomen worden op basis van beperkte data, vaak een steekproef uit het geheel. Statistische besluitvorming is dan de aangewezen werkwijze.
Ter illustratie, er is een nieuw type van een product ontwikkeld. De onderzoekers willen weten of de procesopbrengst van het nieuwe type significant hoger is dan van het oude type. De resultaten worden gemeten in opbrengst per tijdseenheid.
Hoe nu te handelen? De statistische besluitvorming heeft hiervoor een nette procedure, de toetsingsprocedure genoemd. We noemen dit de statistische rechtspraak. Er moet een beslissing genomen worden ‘beyond al reasonable doubt’, maar 100% zekerheid heb je niet.
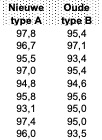
Stap 1: de vraagstelling
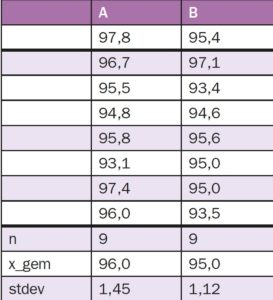
Zo te zien lijkt A wel beter. Gemiddeld is de waarde bij A 96,0 en bij B 95,0, dus je zou kunnen concluderen dat A beter is. Variatie speelt hier echter een belangrijke rol. Kan het verschil ook worden verklaard door normale variatie, in de volksmond ook wel ‘toeval’ genoemd?
Stap 2: uitgangspunten
Om tot een goede formulering te komen hebben we generale uitgangspunten nodig. In deze situatie gaat het om het normale variatiepatroon van het kenmerk. We gaan er in dit voorbeeld vanuit dat dit kenmerk normaal verdeeld is met gemiddelde μAvoor de nieuwe en gemiddelde μBvoor de oude situatie. Verder nemen we aan dat de variatie voor beide in omvang gelijk is, namelijk met een standaarddeviatie σ.
Stap 3: de formulering
Allereerst formuleren we de aanklacht in de vorm van de parameters, waarbij we ongelijkheid als misdrijf beschouwen. Onschuld is dus gelijkheid van de parameters en eigenlijk willen we dat beyond all reasonable doubtverwerpen. De formulering van gelijkheid noemen we de Nulhypothese H0: μA= μB. terwijl het alternatief wordt gevorm door Ha: μA≠μB. Nu kunnen we niets met zekerheid zeggen want het zou kunnen zijn dat we ten onrechte het besluit nemen dat de gemiddelden niet gelijk zijn aan, maar dat we door de variatie in de data wel tot die beslissing komen. Deze fout in de besluitvorming kunnen we echter beheersen, meestal wordt de kans daarop op 5% gezet. We noemen dat de onbetrouwbaarheidsdrempel a=0,05.
Stap 4: het beoordelingsinstrument
Ieder type vraagstuk is uniek en behoeft dan ook een specifiek beoordelingsinstrument. In de inleiding keken we al naar het verschillen van de gemiddelden van de data in de steekproef en dat lijkt zeer voor de hand te liggen. Maar daarbij werd geen rekening gehouden met de variatie in de data. Om tot een goede beoordeling te komen moeten we dus eigenlijk kijken naar het verschil in gemiddelden tegen de achtergrond van de te verwachte variatie in dat verschil, gegeven de data. Dit wordt tot uitdrukking gebracht in wat we noemen de toetsingsgrootheid die past bij deze specifieke situatie. Die ziet er als volgt uit:
Zoals je ziet wordt het gemiddelde verschil gerefereerd aan de variatie (weergegeven in het kwadraat van de standaarddeviaties in de data bij A: sAen bij B: sB). Is het verschil groter dan je zou verwachten op basis van de normale variatie, dan is er voldoende overtuigingskracht om dat aan te nemen. In de formules zijn nAhet aantal waarnemingen bij A en nBhet aantal waarnemingen bij B, in ons voorbeeld dus beide gelijk aan 9.
Stap 5: grenzen stellen
Als de nulhypothese waar is, dan verwacht je dat de gemiddelde waarden bij A en B ook gelijk zijn aan elkaar en dus is naar verwachting de waarde van de toetsingsgrootheid gelijk aan 0. Door de optredende variatie zal deze echter altijd wel een beetje van 0 verschillen, maar waar liggen de grenzen? Wanneer geloof je niet meer in de juistheid van de nulhypothese?
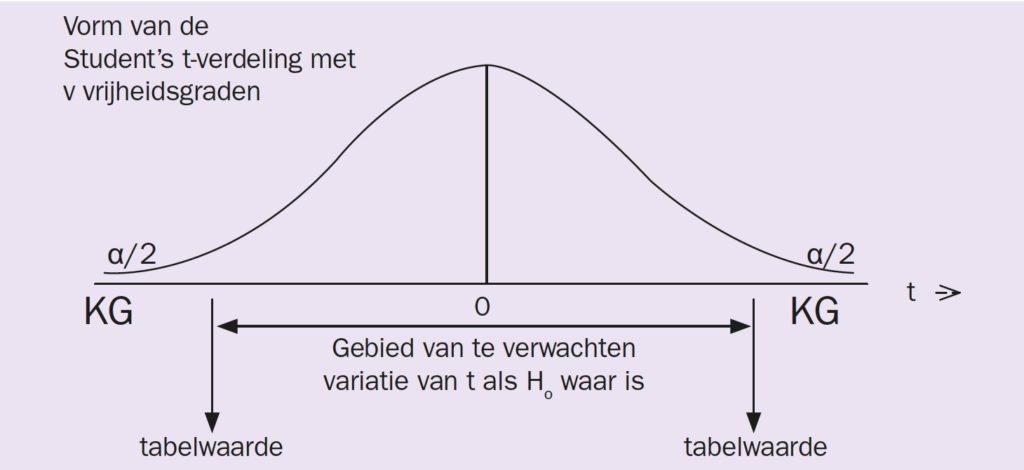
Er zijn twee situaties te bedenken: als t heel veel verschilt van 0 in hoge negatieve waarde en als t verschilt van 0 in hoge positieve waarde.
Om dat te beoordelen hebben we twee dingen nodig. Ten eerste inzicht in het normale variatiegedrag van de toetsingsgrootheid t. Ten tweede (maar die hebben we al) een uitspraak over de kans om de verkeerde beslissing te nemen. Deze laatste hebben we al aangegeven met de onbetrouwbaarheidsdrempel a(=0,05). Omdat we eigenlijk twee foute beslissingen kunnen nemen (fout 1: μA< μB; fout 2: μA> μB), verdelen we de risico’s over twee gebieden, ieder 0,025.
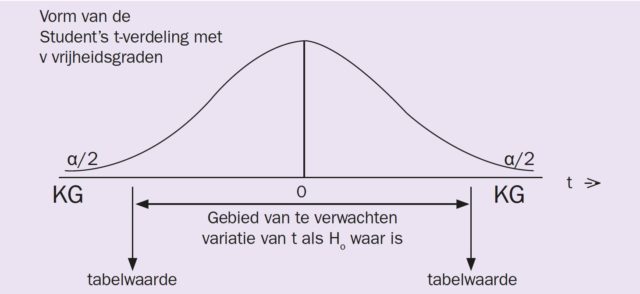
Nu moeten we ons beroepen op het onderzoekswerk van de statistici. Dat heeft opgeleverd dat het normale variatiegedrag van onze toetsingsgrootheid t een speciale vorm volgt, weergegeven als de Student’s t-verdeling. Deze kunnen we (net als de bijvoorbeeld de normale verdeling) in tabellen weergeven of in Excel berekenen. Er zijn heel veel verschillende vormen van deze verdeling en die hangen samen met het aantal waarnemingen dat is gedaan. We geven dat aan met het aantal vrijheidsgraden u=nA+nB-2.
Waar ligt nu de grens? Eigenlijk zeggen we dat als een waarde van t heel veel van de verwachtte waarde 0 verschilt, in positieve of negatieve waarde, dat we dan het uitgangspunt van gelijkheid ongeloofwaardig vinden. Het zou alsnog zo kunnen zijn, maar de kans dat we zo’n grote positieve of negatieve waarde krijgen als Howaar is, is wel heel erg klein. En dat is de basis voor de formulering van de grenzen; ‘heel erg klein’ maken we concreet met de waarde van de onbetrouwbaarheidsdrempel. De waarden van t met een te kleine kans op realisatie onder H0noemen we het Kritieke Gebied KG.
Gegeven de Student’s t verdeling kunnen we nu ook de grenswaarden van t bepalen zodat de kans dat t voorbij deze waarden komt gelijk is aan 0,025 aan beide zijden. Uit de tekstboekjes blijkt dan dat deze grenswaarde gelijk is aan -2,119 en 2,119.
Stap 6: bepaling uitkomst
Op basis van de data kunnen we nu de uitkomst van t berekenen: t = 1,654.
Stap 7: het oordeel
De waarde van de toetsingsgrootheid ligt niet voorbij de grenswaarde. Het is dus niet overtuigend aangetoond dat A verschilt van B. Het optredende verschil in gemiddelde waarden kan goed aan de aanwezig variatie (het toeval) toegewezen worden.
Arend Oosterhoorn begeleidt vanuit zijn eigen adviespraktijk organisaties die op zoek zijn naar verbetermogelijkheden.
Kijk hier voor meer Kwaliteitsinstrumenten!Â
