Een meetsysteemanalyse is een systematische inschatting of de metingen of gepresenteerde data voldoende betrouwbaar zijn om conclusies op te baseren. Betrouwbaarheid wordt uitgedrukt in termen als nauwkeurigheid en herhaalbaarheid. Oftewel: zijn de waarnemers in staat om bij een gelijke waarneming ook wederkerig en onderling gelijkend een meting te verrichten?
Hoe werkt het?
Om de mate van variatie van het totale meetproces vast te stellen, wordt gekeken naar drie belangrijke bronnen van variatie
- variatie ten gevolge van het meetsysteem (Herhaalbaarheid of Equipment Variation, EV);
- variatie ten gevolge van de menselijke verschillen (Reproduceerbaarheid of Appraiser Variation, AV);
- variatie ten gevolge van de verschillen tussen producten (Product Variation, PV).
Om die variatiebronnen te kunnen inschatten worden op de volgende wijze data verzameld:
- laat m operators (meestal m=3)
- ieder n producten (meestal n=10)
- elk r keer meten (meestal r=3).
Voorbeeld
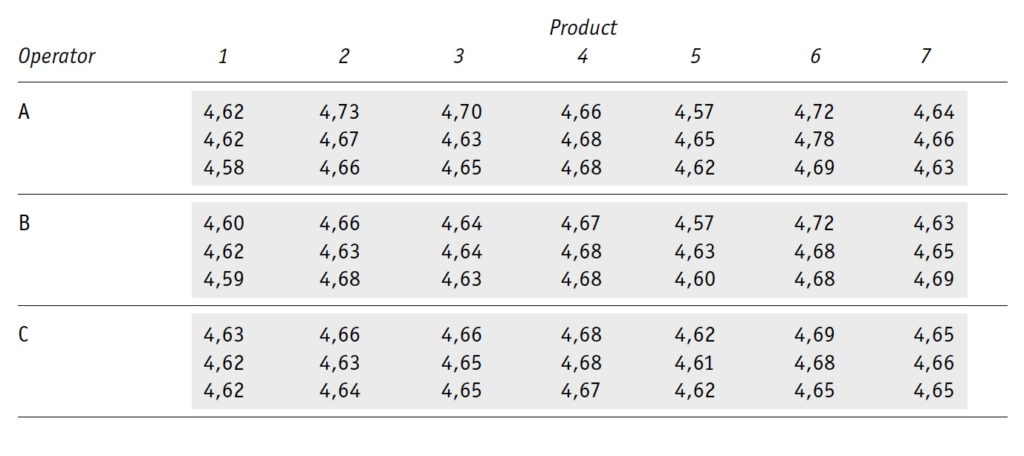
Voor het voorbeeld nemen we 3 operators, 7 producten en 3 herhaalde metingen. Dat geeft het volgende schema:
Aanpak
De uitspraak van het onderzoek moet zo algemeen geldend mogelijk zijn. Daarvoor moeten de operators die het werk verrichten en de producten die worden gebruikt zoveel mogelijk overeenstemmen met de latere situatie.
1. Selecteer het gewenste aantal operators die de metingen moeten uitvoeren. Dit moeten vooral mensen zijn die normaal gesproken ook de metingen verrichten. Als dat niet mogelijk is, laat dan in ieder geval iemand de metingen verrichten die gevoel heeft voor het product en de meting. Een resultaat van een totaal vreemde operator, die later nooit meer iets met die meting zal doen, is niet zo relevant.
2. Selecteer het gewenste aantal producten voor het uitvoeren van de studie. Deze producten moeten qua variatie in het te meten kenmerk representatief zijn voor de normale situatie. Selecteer ze dus niet als n producten direct na elkaar geproduceerd, dan is er onvoldoende variatie tussen de producten. Ga voor de selectie eerst na aan de hand van historische data hoeveel variatie er normaal aanwezig is, bijvoorbeeld ten gevolge van verschillen tussen machines, ploegen, operators, leveranciers en dergelijke. Zorg dat de producten die gebruikt worden voor het onderzoek daarvoor representatief zijn.
3. Verzorg enige administratie rondom de producten (herkomst, identificatie), het meetmiddel (serienummer, kalibratiedatum, …), de medewerkers die de metingen verrichten (naam, afdeling) en omstandigheden (geconditioneerde ruimte, tijd tussen metingen, werkwijze bij metingen). Dit om ervoor te zorgen dat de resultaten na enige tijd nog herleidbaar en te interpreteren zijn.
Opmerking
Bij destructieve metingen is het niet mogelijk herhaalde metingen te verrichten aan de producten. De enige uitweg is om in plaats van herhalingen aan hetzelfde product, metingen te verrichten aan r opeenvolgend geproduceerde producten. Dan zit er tussen die meetresultaten een beetje meer variatie dan alleen op basis van meetapparaat, maar deze manier is in een dergelijk geval de beste.
Tussenresultaten
Voor de analyse zijn op basis van de meetwaarden enige tussenresultaten nodig. Deze worden direct uit de waarnemingen afgeleid.
Het gaat om:
- de variatie ten gevolge van de meetapparatuur, die is verpakt in de ranges tussen de r metingen per operator/product en die wordt samengevat in de gemiddelde waarde van al deze (m × n) ranges;
- de variatie tussen de operators, die tot uiting komt in de verschillen tussen de gemiddelde waarden per operator en die wordt uitgedrukt in de range van de gemiddelden per operator;
- de variatie tussen de producten, die tot uiting komt in de variatie in de gemiddelde waarde per product en die wordt uitgedrukt in de range van de productgemiddelden.
Voorbeeld
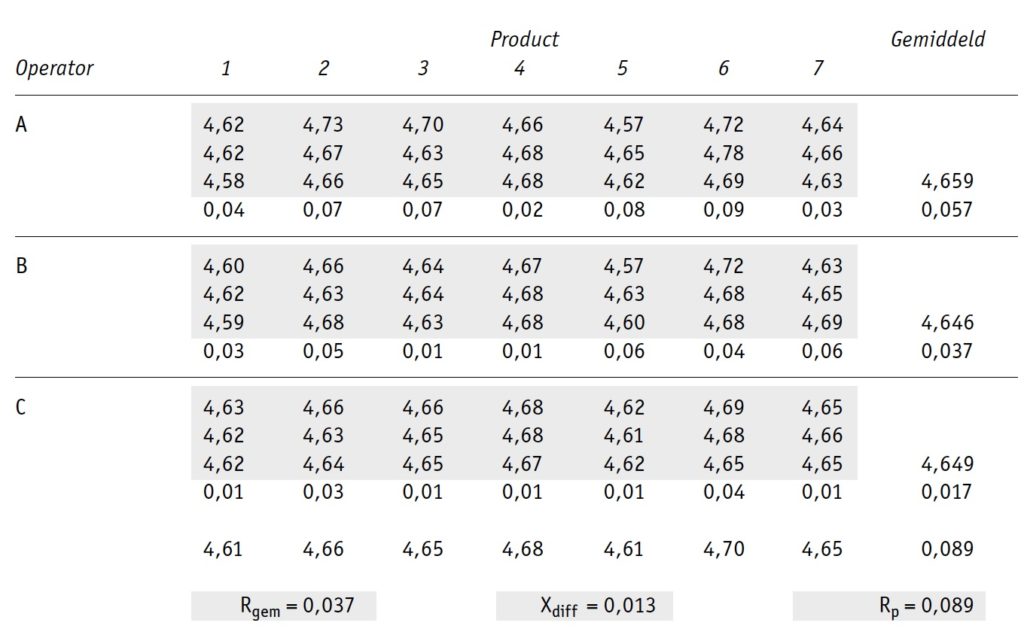
Voor de data van het voorbeeld gelden de volgende resultaten:
Aanpak
1. Bereken per r metingen per operator/product de range. Dit geeft m × n ranges. De gemiddelde waarde daarvan wordt samengevat in Rgem.
2. Bereken per operator de gemiddelde waarde van de gemeten waarden. De range tussen deze gemiddelden wordt samengevat in Xdiff.
3. Bereken de gemiddelde waarden per product, over alle metingen van dat product (herhalingen en operators). Bereken de range tussen deze gemiddelden en ken dat toe aan Rp.
In de tabel kan – ook met het oog op verdere analyse – het gemiddelde per product per operator nog worden opgenomen.
Bron: 111 Instrumenten voor kwaliteitsverbetering, Arend Oosterhoorn