Onlangs vroeg een strandtenthouder of er een verband bestaat tussen de voorspelde temperatuur in het weekend en het bierverbruik. Hij zou de bieromzet dan beter kunnen voorspellen en voorkomen dat het bier aan het einde van de middag al op is. Hoe kunnen we deze samenhang meten?
Al eerder hebben wij bij kwaliteitsinstrumenten we al eens gesproken over de mate van samenhang tussen verschillende variabelen. Zie bijvoorbeeld ‘Aannemelijk maken van samenhang‘ ( (Sigma 3, juni 2014) en ‘Kruistabellen en onafhankelijkheid‘ (Sigma 2, juli 2018).
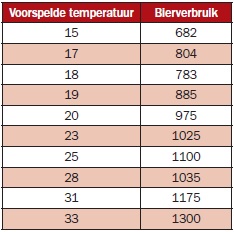
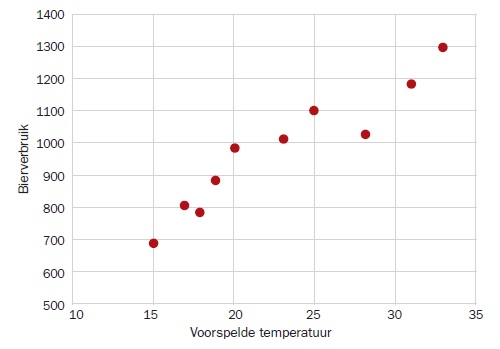
Een tijdlang hebben we de weersverwachtingen gevolgd en de bierhoeveelheid gemeten (er is wel een en ander op te merken over de opzet van dit onderzoek, maar het gaat nu over de methodiek). Uitgezet in een grafiek lijkt er wel sprake van enige mate van samenhang. Verwijzend naar het artikel van juni 2014: de waarde van de correlatiecoëfficiënt is gelijk aan 0.952.
Als we weten dat er sprake is van samenhang ontstaan twee vragen. De eerste is fundamenteel: snappen we het achterliggende mechanisme dat deze samenhang veroorzaakt? Want uit alle datasets is wel een correlatiewaarde te berekenen, maar dat zegt nog niet zo veel. Begrijpen wat er gebeurt, geeft de garantie dat je geen onzinuitspraken gaat doen. In het geval van temperatuur en bier is een dergelijk mechanisme verdedigbaar.
De tweede vraag is meer praktisch en betreft de vorm van de samenhang. Als we deze vorm kunnen samenvatten in een formule, dan kunnen we op basis van de uitgangsdata ook voorspellingen doen. Dat maakt het voorspelbaar en veel makkelijker om afwijkingen waar te nemen en daardoor te leren.
Analyse in vier stappen
Er zijn vier stadia in de analyse die standaard worden uitgevoerd. Ten eerste wordt gekeken naar het model dat zou moeten worden gehanteerd en waarmee het mechanisme kan worden beschreven. In veel gevallen (en ook in dit geval) gaan we uit van de veronderstelling dat er recht evenredig meer gedronken zal gaan worden naarmate de temperatuur stijgt (binnen het gebied van de meetwaarden, want het is onwaarschijnlijk dat mensen bij veel vorst bier terug komen brengen). De vergelijking van een rechte lijn is Y = α + βX, ofwel de toename per graad temperatuur isβ liter. De waarde van vertegenwoordigt het snijpunt van deze rechte lijn met de Y-as als X = 0.
Als we ervan uitgaan dat we binnen het meetgebied daadwerkelijk het drinkgedrag afhankelijk van de temperatuur kunnen beschrijven met een rechte lijn, dan is de volgende vraag hoe we de best passende lijn bepalen bij de gegeven meetresultaten.
Daarvoor zijn binnen de statistiek de nodige formules uitgevonden (zie kader).
Merk op dat we spreken over a en b als we de waarde van α en β schatten op basis van de data. De parameters α en β behoren tot het model, de waarden van a en b zijn de op basis van de data geschatte waarden (en dus enige mate onzeker).
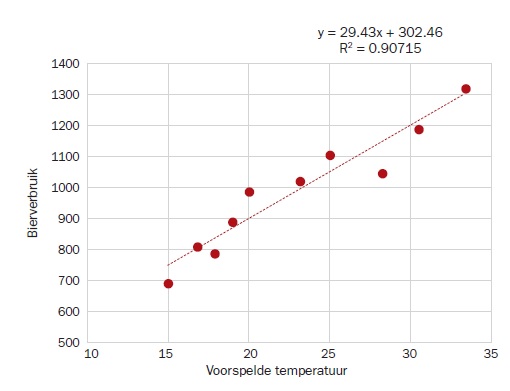
Als we die waarden eenmaal hebben geschat, kunnen we deze best passende lijn in de grafiek zetten en zien hoe de data passen bij deze rechte lijn.
De volgende stap is te bepalen hoe goed het model en de data bij elkaar passen. Daarvoor bestaat de passingsmaat R2. Dat is de verhouding tussen de mate van variatie in de Y-waarden zonder rekening te houden met de samenhang en de variatie van de residuen, zijnde de ‘overblijvende’ variatie na rekening te houden met het model. Deze R2-waarde geeft het percentage verklaarde variatie in de Y-waarden aan door toepassing van het model. Hoe dichter bij 1 (100%), hoe sterker de binding tussen data en model. Een R2 van 0.907 geeft aan dat we 90% van de variatie in het bierverbruik kunnen verklaren, rekening houdend met de variatie in de voorspelde temperatuur.
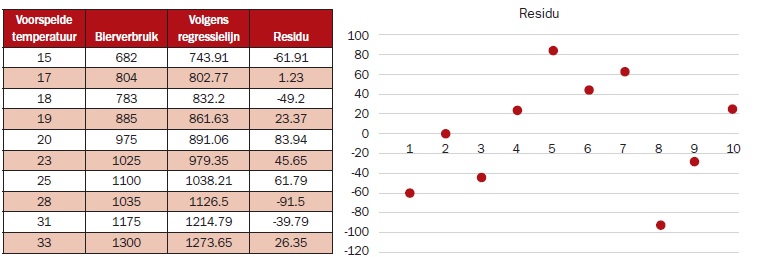
Rest ons te leren van de afwijkingen. We kunnen per datapunt bepalen wat de waarde was volgens de lijn (a + bX) en wat de waargenomen waarde van Y is. Het verschil noemen we een residu en die geeft informatie over de mate waarin het model past bij de data (en niet andersom).
Berekenen van deze residuen (standaard weergegeven door de letter e) gaat dus door Y – (a + bX) te bepalen voor alle data. Grafisch kunnen we deze dan ook weergeven.
In Excel gaat dat redelijk eenvoudig. De data geef je weer in een spreidingsdiagram, de X-waarden op de X-as en de Y-waarden op de Y-as, punten weergegeven als stippen. Daarna selecteer je een punt in de grafiek, waarna de hele datareeks wordt geselecteerd (zie je ook omdat er meerdere stippen worden geselecteerd). Je drukt op de rechtermuisknop en selecteert uit het menu Trendlijn toevoegen. In dat menu kies je voor lineair (rechte lijn) en vinkt de keuzes aan ‘vergelijking in de grafiek weergeven’ en ‘R-kwadraat in de grafiek weergeven’. Dan komen beide resultaten in de grafiek zichtbaar in beeld.
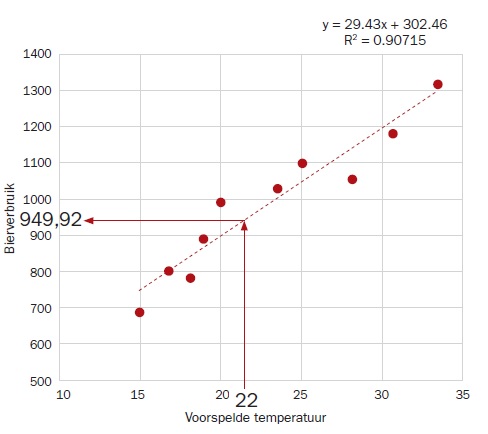
Nu kun je deze kennis gebruiken om voorspellingen te doen. Als bijvoorbeeld een temperatuur van 22 graden wordt voorspeld, verwachten we een bierverbruik van 302.46 + 29.43 * 22 = 949.92.
Er is een aantal opmerkingen te maken:
- Er moet bij deze aanpak wel altijd een achterliggende gedachte zijn over het toe te passen model. Vaak zien we grafieken waar de maker een mooie lijn (recht, parabolisch, golvend, ….) doorheen heeft getrokken. Excel is geduldig, die doet gewoon wat je ingeeft. Maar als je dan vraagt naar het achterliggende mechanisme dat door de gekozen lijn wordt weergegeven, wordt het stil. Dus zorg dat je alleen overgaat op het toevoegen van dergelijke modelweergaven als je dat ook kunt verklaren of daarnaar op zoek bent.
- De waarde van a + bX geeft de verwachte waarde aan bij een gegeven waarde van X, volgens het model. Daarmee verklaren we de waarde van Y slechts met één andere variabele (X). Maar de waarde van Y zal ongetwijfeld worden beïnvloed door meerdere variabelen. Deze invloed zie je terug in de residuen. Vandaar dat deze residuenanalyse zo belangrijk is. Deze onzekerheid geven onze weermensen aan met ‘de pluim’.
- Dit model zouden we al kunnen verbeteren door in plaats van de voorspelde temperatuur de werkelijke temperatuur op het terras te meten en in het model op te nemen.
- Deze methode (regressieanalyse genaamd) is veel verder uitgewerkt. Een interessante vorm is bijvoorbeeld een hele rij X’en te meten en te kijken welke van deze X’en de waarde van Y het beste voorspelt. Waardoor wordt het resultaat nu eigenlijk gerealiseerd?
Op deze wijze kun je gebruik maken van veel kwaliteitsgerichte data. Voorspellen van de uitkomst van een proces (Y) aan de hand van wat er in het proces gebeurt (X), maakt dat we meer inzicht krijgen in de dynamiek van een proces en daarmee een betere beheersing kunnen realiseren. Daarmee wordt de kwaliteit van het resultaat voorspelbaar.
Bron: Sigma 3, 2018
Arend Oosterhoorn is al vele jaren actief in de wereld van kwaliteitsmanagement en Lean Six Sigma. Vanuit zijn eigen adviespraktijk begeleidt hij organisaties die op zoek zijn naar verbetermogelijkheden. aoosterhoorn@oosterhoornadvies.nl