Je wil een inventarisatie maken van factoren die mogelijk van invloed zijn op het kenmerk dat je wil onderzoeken. Kun je dat ook aannemelijk maken op basis van data?
Onderzoek naar samenhang is essentieel in het verbeteren van de kwaliteit van producten/diensten en processen. Je moet tenslotte begrijpen hoe de mechanismen werken om het proces te kunnen beïnvloeden en bij te sturen.
Of kenmerken met elkaar samenhangen is statistisch wel aannemelijk te maken, maar je moet er ook een verklaring voor kunnen geven. Er moet een mechanisme zijn dat deze samenhang veroorzaakt. Zo is er een periode dat je salaris toeneemt met het aantal dienstjaren; het achterliggende mechanisme is het gebruik van de salarisschalen per dienstjaar. Er kan ook visueel een aanwijzing zijn, maar zonder verklaring is dat niet veel waard.
Als twee kenmerken met elkaar samenhangen, dan moet het zo zijn dat verandering van de waarde van het ene kenmerk invloed heeft op de waarde van het andere kenmerk. Dat is ook wat we zoeken als het gaat om vaststellen van oorzaak en gevolg uit het visgraatdiagram.
Dit geven we netjes vorm: we onderzoeken de samenhang tussen twee kenmerken (variabelen), waarbij Y de variabele is die het gevolg is van de X variabele. Dus bijvoorbeeld als X (aantal dienstjaren) toeneemt, volgt ook een toename van Y (salaris). Het kan natuurlijk ook andersom, als X toeneemt kan Y afnemen (hopelijk niet bij je dienstjaren en salaris).
Spreidingsdiagram
Om samenhang grafisch weer te geven is eigenlijk alleen maar een spreidingsdiagram van toepassing. In een spreidingsdiagram zetten we de oorzaak (variabele X) op de X-as en het gevolg (variabele Y) op de Y-as. Van iedere entiteit in onze dataset plotten we dan het puntenpaar (x,y) in de grafiek, net zoveel punten als we waarnemingen hebben.
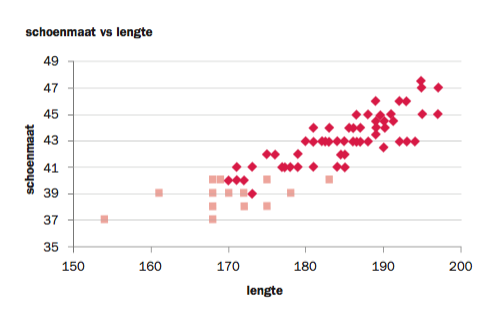
Bijvoorbeeld. Langere mensen hebben waarschijnlijk ook een grotere schoenmaat. Om dat te onderzoeken vragen we verschillende mensen naar hun lengte en naar hun schoenmaat en zetten de resultaten in een spreidingsdiagram. Het lijkt er dus wel op dat naarmate de lengte toeneemt, ook de schoenmaat toe neemt.
Naast deze simpele weergave is het ook mogelijk om bijvoorbeeld onderscheid te maken tussen mannen en vrouwen. In Excel geef je dan twee X-variabelen op, in de ene de data van de mannen en in de andere de data van de vrouwen. Automatisch wordt er dan in twee kleuren een puntenwolk weergegeven (zie figuur).
In versie Excel2013 is het ook mogelijk om de punten te voorzien van een individueel label dat in de grafiek zicht-baar wordt. Via Gegevenslabels -> Meer opties -> Labelopties -> Waarde uit cellen geef je de datareeks op waar de labels staan van deze waarnemingen, deze worden dan bij ieder punt weergegeven. Met name bij afwijkende waarnemingen in de grafiek is dat makkelijk, je kunt direct terugzien welke waarnemingen het betreft.
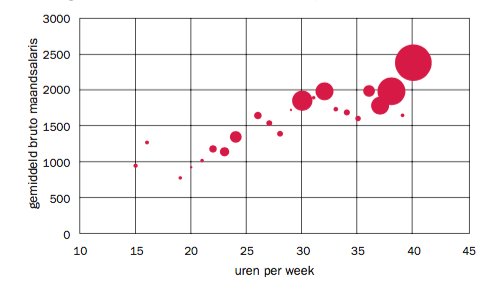
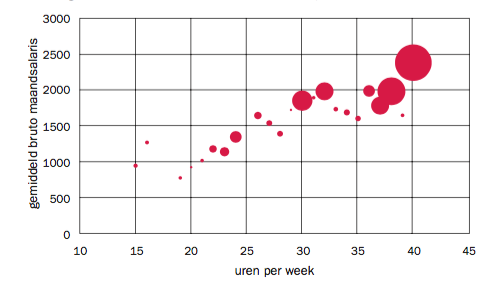
Bellengrafiek
Het komt ook voor dat je van bepaalde combinaties meerdere waarnemingen hebt. Dan maak je een bellengrafiek. Dat is ook een spreidingsdiagram, maar de punten worden dan ‘opgeblazen’, al naar gelang er meerdere waarnemingen zijn van bepaalde combinaties. Dit werkt bijvoorbeeld erg goed als je de gemiddelden van de ene variabele (bijvoorbeeld bruto maandsalaris) uit wilt zetten tegen de waarde van een andere (bijvoorbeeld aantal werkuren per week). Het aantal waarnemingen in iedere klasse van werkuren is dan de ‘opblaasfactor’.
Samenhang is niet alleen grafisch weer te geven, het is ook samen te vatten in een kengetal, de zogenoemde correlatiecoëfficiënt. Ik zal u niet bezwaren met formules, maar slechts verwijzen naar de berekeningswijze in Excel. De correlatiecoëfficiënt is een getal tussen -1 en + 1 en in de buurt van 0 is er geen sprake van samenhang. Naarmate de correlatiecoëfficiënt dichter bij -1 of +1 komt, is de samenhang sterker. Als de correlatiecoëfficiënt kleiner dan nul is, spreken we van een negatieve correlatie (de waarde van Y neemt af als de waarde van X toeneemt), is deze groter dan nul dan dui- den we dat aan als positieve correlatie (de waarde van Y neemt toe met toenemende waarde van X). Er bestaan tabellen die aangeven wat de ondergrens is voor de waarde voordat je mag spreken van echte samenhang (uiteraard in combinatie met de verklaring). Ter illustratie, de samenhang tussen schoenmaat en lengte voor alle personen gezamenlijk komt uit op 0,82.

