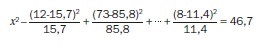De kappa-waarde is een maat voor overeenstemming tussen beoordelaars bij subjectieve beoordelingen. Deze maakt gebruik van de 2×2 tabel, een kruistabel geheten binnen de statistiek.
Veel procesbeoordelingen worden gedaan op basis van tellingen in combinatie met categorieën. Zo tellen we valincidenten ingedeeld naar aard, beschadigingen naar vorm, klachten naar herkomst enzovoort. Als we deze willen verklaren om een incident te voorkomen, moeten we deze data koppelen aan de herkomst of locatie. Bijvoorbeeld de verdeling van valincidenten bekeken per afdeling of locatie, aard van beschadigingen of type klachten onderverdeeld naar herkomstproces.
Lees hier de voorgaande bijdrage: ‘Overeenstemming bereiken tussen beoordelaars‘
Laten we eens kijken naar een (fictieve) zuivelfabriek. Het probleem is dat er aan het einde van de lijn waar pakken zuiveldrank worden afgevuld, regelmatig beschadigde pakken uitkomen. Iedere zuiveldrank wordt op een aparte lijn afgevuld. De vraag is of de lekkages veroorzaakt worden door mechanismen die onafhankelijk zijn van de lijn waar ze geproduceerd worden of dat het mechanisme afhankelijk is van de lijn.
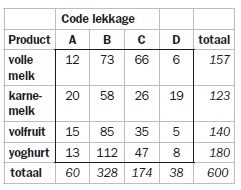
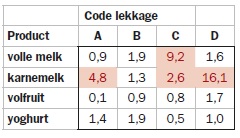
Hoe gaan we dan te werk? Het start met data verzamelen. In algemene termen worden dit de waargenomen waarden genoemd.
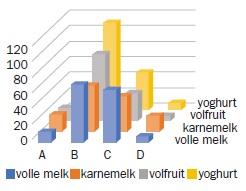
Bij hoge uitzondering geven we dit ook weer in een 3D-kolomdiagram, om een beter beeld te krijgen van de situatie.
Onafhankelijk van de lijn
We kijken eerst vanuit de veronderstelling van onafhankelijkheid, dus dat de mechanismen voor het beschadigen van de pakken bij alle lijnen gelijk is. Gegeven de randtotalen kunnen we berekenen welke verdeling over de lekkagecodes we zouden verwachten voor iedere lijn. Als het namelijk niet uitmaakt, verwacht je dat voor de vier lijnen de verhouding over de vier lekkagecodes gelijk is en wel volgens de verhouding 60:328:174:38.
Voor lekkagecodes van volle melk zou je dan ook die verhouding verwachten. De 157 lekkages die gevonden zijn bij volle melk zouden naar rato verdeeld zijn over lekkagecode A, B, C en D. Dus 60/600-ste van de 157 (=15,7) verwachten we bij volle melk voor lekkagecode A, 328/600-ste van de 157 (=85,8) verwachten we bij B enzovoort.
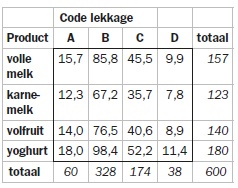
Doen we dat voor de hele tabel, dan volgt de tabel met verwachte aantallen onder de veronderstelling van onafhankelijkheid (het zijn rekenresultaten, dus 15,7 beschadigde pakken is mogelijk).
Je ziet dat vooral de karnemelklijn afwijkt van het patroon. Dat zie je ook al een beetje in de grafiek en het wordt bevestigd door de verschillen in waargenomen waarden en verwachte waarden onder aanname van onafhankelijkheid.
Om nu na te gaan of die verschillen op toeval berusten of dat er een gerechtvaardigde verdenking is dat er iets anders aan de hand is bij de karnemelklijn, berekenen we een waarde gebaseerd op deze verschillen, de zogenaamde chi-kwadraatwaarde.
Voor dit voorbeeld volgt dan
Interessant is te kijken waar nu de grote afwijkingen zitten. Daarvoor kunnen we een aparte tabel maken met de waarden (waargenomen – verwacht)2/verwacht per cel.
Ook daar zie je dat de afwijkingen bij karnemelk tot de 25% grootste afwijkingen behoort. Er lijkt iets aan de hand te zijn bij de karnemelklijn.
Nu komt de vraag waar de grens ligt: wanneer besluiten we dat de basisveronderstelling van onafhankelijkheid niet meer houdbaar is?
Als de waargenomen waarden heel dicht bij de verwachte waarden ligt, zal de chi-kwadraat klein zijn, allemaal kleine verschillen die optellen. Wijken de waargenomen waarden (ver) af van de verwachte waarden onder onafhankelijkheid, dan zijn de verschillen natuurlijk groot en zal de chi-kwadraat ook (heel) groot zijn.
Nu weten we binnen de statistiek wat het gedrag van deze chi-kwadraatwaarde is onder die veronderstelde onafhankelijkheid, deze volgt een zogenaamde chi-kwadraatverdeling (zoiets als de normale verdeling, maar dan een andere vorm). Als we de verdeling kennen, kunnen we kansen uitrekenen. Zo is het mogelijk om de kans uit te rekenen om een waarde te krijgen die groter of gelijk is aan de waarde die we hebben gevonden uit de data.
Daar moet dan nog wel een tussenbepaling bij. Als er veel meer lekkagecodes zijn en/of meer lijnen, neemt het aantal cellen toe en kun je ook een grotere waarde van deze chi-kwadraat verwachten. Dat wordt gecompenseerd doordat de chi-kwadraatverdeling afhankelijk is van het aantal vrijheidsgraden. Voor deze situatie is dat gelijk aan:
(aantal rijen – 1) x (aantal kolommen – 1) = (4 – 1) x (4 – 1) = 9.
Nu kunnen we die kans uitrekenen. Vroeger moesten we dat in tabellen opzoeken, maar gelukkig staat daar Excel nu voor paraat. Via de functie:
=CHI.KWADRAAT(x ; vrijheidsgraden)
Deze kans weerspiegelt de waarschijnlijkheid dat we de gevonden waarde verkrijgen onder de veronderstelling van onafhankelijkheid; het mechanisme van beschadigingen is voor alle lijnen dezelfde. Als die kans heel klein is, wordt de basisveronderstelling van onafhankelijkheid dus ook onwaarschijnlijk en kunnen we concluderen dat het meest waarschijnlijk is dat er een afwijkend mechanisme is in ten minste één van de lijnen (de karnemelklijn is de meest voor de hand liggende kandidaat).
Merk op dat het allemaal voorzichtig is geformuleerd. Vanuit de statistiek kunnen we geen absolute zekerheid verschaffen, maar slechts meest waarschijnlijke richtingen aangeven of onwaarschijnlijke verklaringen pareren.
In dit geval wordt deze kans berekend:
=CHI.KWADRAAT(46,7 ; 9) = 0,00000045
Ofwel: 4,5 maal per 10.000.000. Het lijkt dus zeer onwaarschijnlijk dat de mechanismen voor alle lijnen gelijk zijn en daarmee opteren we voor het alternatief.
In de dagelijks praktijk is een waarde van deze kans, de zogenaamde p-waarde, kleiner dan 0,05 al genoeg om aan de basisveronderstelling van onafhankelijkheid te gaan twijfelen. In dit geval is het dus al veel overtuigender dat er bij de karnemelklijn iets bijzonders aan de hand is.
Gelukkig hoeven we dat niet allemaal handmatig te berekenen. Excel heeft een functie die deze p-waarde voor je berekent op basis van de tabellen.
=CHI.TOETS(waarnemingen ; verwacht)
waarbij waarnemingen de tabel is met de teldata en verwacht de tabel met de berekende verwachte waarden (die moet je nog wel zelf berekenen).
Zo kunnen we een door data gerechtvaardigd onderzoek starten naar de verschillen tussen de lijnen om te achterhalen welke mechanismen er spelen die lekkages veroorzaken en hoe we deze kunnen elimineren.
door Arend Oosterhoorn, zelfstandig kwaliteitsadviseur
Lees hier de voorgaande bijdrage: ‘Overeenstemming bereiken tussen beoordelaars‘