De Box- en Whiskergrafiek biedt overzicht van data uit verschillende bronnen. Het laat variatie en grootte zien in één grafische voorstelling. Door de heldere weergave kun je met deze grafieken eenvoudig data uit verschillende categorieën vergelijken.
In een vorige bijdrage is het histogram besproken, de grafische weergave van variatie in data. Het histogram biedt helder inzicht, maar het beperkt zich tot een totaal van de data. Als er echter sprake is van verschillende categorieën, locaties, groepen, bewerkingsplekken en dergelijke, dan wordt het lastiger om de variatie over de verschillende groepen te vergelijken. Uiteraard is het mogelijk om meerdere histogrammen te maken, maar dat is veel werk.
Box & Whisker
Een alternatief is het maken van een box- en whiskerplot (John Tukey, 1977). Daarin is het mogelijk om de ligging en de mate van spreiding van de data over de verschillende groepen in één grafische weergave te plaatsen. Maar daarvoor hebben we eerst iets anders nodig.
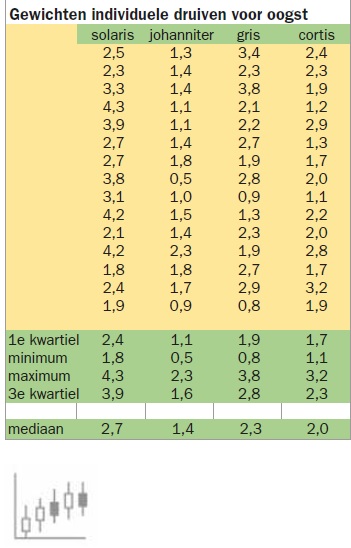
Stel, we hebben een rij data en willen deze typeren in kengetallen. Gemiddelden voor de grootte en standaarddeviatie voor de variatie zijn wellicht bekend, maar de box- en whiskerplot maakt gebruik van de mediaan en het eerste en derde kwartiel.
De mediaan is de waarde die de dataset in twee gelijke delen qua aantallen verdeelt, zeg maar het 50%-punt. Het eerste kwartiel doet hetzelfde met de eerste 50%, het derde kwartiel met de tweede 50%. Zo valt tussen het eerste kwartiel en het derde kwartiel de middelste 50% van de data.
Constructie van de box & whisker
Op de plaats van de mediaan trekken we een streepje (of zetten we een boxje). Tussen de waarde van het eerste kwartiel en het derde kwartiel tekenen we een rechthoek (box) en dan gaat het nog om de weergave van de whiskers (snorharen).
Daar ontstaat een keuze. De makkelijkste is om de eerste snorhaar als lijn te tekenen van het minimum tot de rand van de box bij het eerste kwartiel en de tweede snorhaar vanaf de box bij het derde kwartiel tot het maximum. Een alternatief is om het maximum en het minimum te vervangen door een aantal maal de standaarddeviatie vanaf de mediaan.
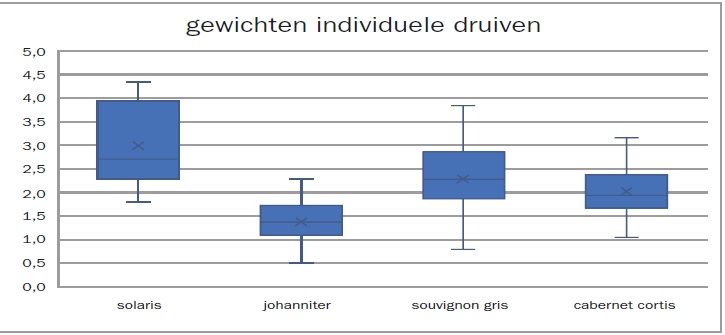
Excel (2016 en hoger) berekent voor de lengte van de snorharen maximaal 1,5 maal de interkwartielrange (derde kwartiel minus eerste kwartiel). Alles wat daarbuiten valt, wordt als uitschieter weergegeven in de vorm van een ster. In statistische softwarepakketten is dat in te stellen, bij Excel gaat dat (nog) niet. Met Excel gaat dat als volgt. Er bestaat de functie =MEDIAAN(databereik). Tevens bestaan de functies =KWARTIEL(databereik;1) voor het eerste kwartiel en =KWARTIEL(databereik;3) voor het derde. Uiteraard hebben we ook nog =MAX(databereik) voor het maximum en =MIN(databereik) voor de minimumwaarde.
Excel versie 2013 of lager heeft geen standaard box- en whiskerplot, maar er kan via een open/hoog/laag/slotgrafiek wel iets eenvoudigs geconstrueerd worden zodat er een helder beeld ontstaat. Dat gaat via de volgende werkwijze:
- maak per categorie een kolom met daarin de data;
- bereken onder elkaar per datakolom 1e kwartiel, minimum, maximum en 3e kwartiel;
- selecteer de data, neem daarin de namen van de categorieën mee in de eerste rij;
- selecteer de grafische weergave open/hoog/laag/slot.
De weergave heeft niet de positie van de mediaan in de weergave, maar er ontstaat wel een beeld omtrent de verschillen in ligging van de data en de mate van variatie.
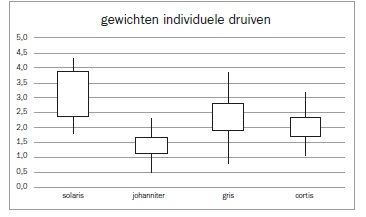
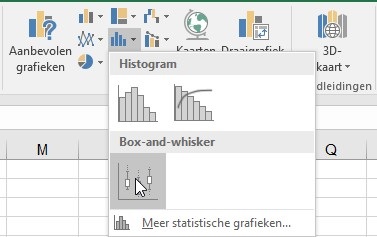
Voor mensen met een versie van Excel 2016 of hoger wordt het leven nu wat eenvoudiger. Deze versies hebben standaard box- en whiskerplot in de grafische mogelijkheden. Daarvoor moeten de data anders worden georganiseerd. In de ene kolom staat de categorie aanduiding (hoeft niet gegroepeerd te zijn) en in de tweede kolom staan de weer te geven data. Nu selecteren we de twee datakolommen en kiezen voor de box en whisker. De grafiek ontstaat direct.
Wat heb je nu aan deze grafische weergave?
Het geeft je inzicht in de onderlinge verschillen in de waarden van de te onderzoeken eigenschap. Tevens kun je door de lengte van de boxen en/of de lengte van de snorharen de verschillen in de mate van variatie zien. Kleine boxen betekenen relatief weinig variatie, zien we grotere boxen dan liggen de 50% middelste data dus verder uit elkaar en is er sprake van meer variatie.
In het voorbeeld van de gewichten van individuele druiven zien we dat de Solaris druiven zwaarder zijn, maar ook de meeste variatie vertonen. De Johanniter druiven wegen het minst met ook de geringste variatie. Sauvignon Gris en Cabernet Cortis verschillen niet veel van elkaar.
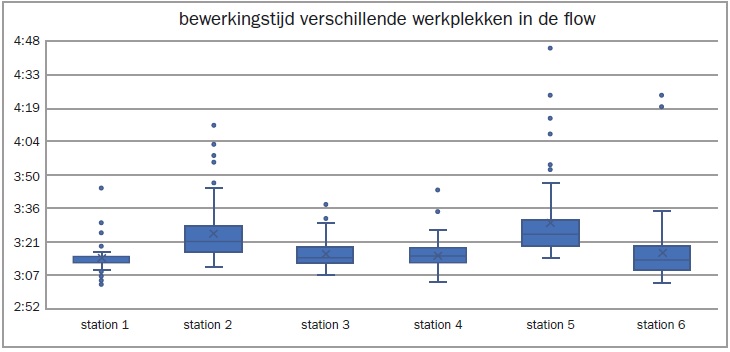
Dit is een wat van de kwaliteitspraktijk afwijkend voorbeeld, maar toepassingen zijn er te over van deze grafische voorstelling. Zo kun je de doorlooptijden van verschillende stations in een workflow goed zichtbaar maken. Ook hier zie je in één oogopslag de verschillen in doorlooptijden per station. Station 1 heeft weinig variatie en weinig tijd, station 5 is waarschijnlijk de bottleneck, mogelijk soms in combinatie met station 2.
Excel 2016 heeft twee aparte versies van de functie =KWARTIEL, namelijk =KWARTIEL.INC() en =KWARTIEL. EXC(). Bij de eerste wordt bij een oneven aantal waarnemingen de kwartielwaarde berekend over de data waar de mediaan is meegenomen; bij de tweede wordt de mediaanwaarde buiten beschouwing gelaten. Bij grafieken op basis van kleine datasets kan dat een afwijkend beeld geven; als de omvang van de dataset toeneemt, dan maakt het niet zoveel uit.
Arend Oosterhoorn is al vele jaren actief in de wereld van kwaliteitsmanagement en Lean Six Sigma. Vanuit zijn eigen adviespraktijk begeleidt hij organisaties die op zoek zijn naar verbetermogelijkheden.
Bron: Sigma, nr. 4 september 2017